Thể tích nước của một bể bơi sau t phút bơm tính theo công thức $V\left( t \right)=\dfrac{1}{100}\left( 30{{t}^{3}}-\dfrac{{{t}^{4}}}{4} \right)$ (lít) với $\left( 0\le t\le 90 \right)$. Tốc độ bơm nước tại thời điểm t được tính bở công thức $f\left( t \right)=V’\left( t \right)$. Xác định tính đúng/sai của các khẳng định sau:
a) Tốc độ bơm giảm từ phút thứ 70 đến phút thứ 90.
b) Tốc độ bơm lớn nhất tại thời điểm t = 60 ( phút).
c) Thể tích nước của bể bơi sau 20 phút bơm là 2000 (lít).
d) Tốc độ bơm nước tại thời điểm t là $f\left( t \right)=100\left( 90{{t}^{2}}-{{t}^{3}} \right)$.
Lời giải:
Ta có công thức thể tích nước của một bể bơi sau t phút bơm: $V\left( t \right)=\dfrac{1}{100}\left( 30{{t}^{3}}-\dfrac{{{t}^{4}}}{4} \right)$ (lít) với $\left( 0\le t\le 90 \right)$.
Tốc độ bơm nước tại thời điểm t được tính bởi công thức $f\left( t \right)=V’\left( t \right)$.
Tính đạo hàm bậc nhất của $V(t)$:
$f(t)=V'(t)=\dfrac{1}{100}\left( 30 \cdot 3{{t}^{2}}-\dfrac{4{{t}^{3}}}{4} \right)=\dfrac{1}{100}\left( 90{{t}^{2}}-{{t}^{3}} \right)$.
Tính đạo hàm bậc hai của $V(t)$ (đạo hàm của $f(t)$):
$f'(t)=V”(t)=\dfrac{1}{100}\left( 180t-3{{t}^{2}} \right)$.
Để tìm điểm cực trị của tốc độ bơm, ta giải phương trình $f'(t)=0$:
$\dfrac{1}{100}\left( 180t-3{{t}^{2}} \right)=0$
$180t-3{{t}^{2}}=0$
$3t(60-t)=0$
$\Rightarrow \left[ \begin{array}{l} t=0 \\ t=60 \end{array} \right.$
Lập bảng biến thiên cho tốc độ bơm $f(t)$ trên khoảng $\left[ 0; 90 \right]$:
Khi $0 {
Tính các giá trị của $f(t)$ tại các điểm đặc biệt:
$f(0) = \dfrac{1}{100}(90 \cdot 0^2 – 0^3) = 0$.
$f(60) = \dfrac{1}{100}(90 \cdot 60^2 – 60^3) = \dfrac{1}{100}(90 \cdot 3600 – 216000) = \dfrac{1}{100}(324000 – 216000) = \dfrac{108000}{100} = 1080$.
$f(90) = \dfrac{1}{100}(90 \cdot 90^2 – 90^3) = \dfrac{1}{100}(90^3 – 90^3) = 0$.
Bảng biến thiên của $f(t)$:
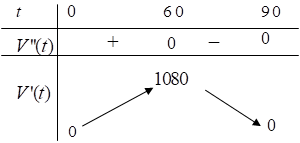
Dựa vào bảng biến thiên và các tính toán:
– **Khẳng định 1:** Tốc độ bơm giảm từ phút thứ 70 đến phút thứ 90.
Theo bảng biến thiên, tốc độ bơm giảm từ phút thứ 60 đến phút thứ 90. Do đó, khẳng định tốc độ bơm giảm từ phút thứ 70 đến phút thứ 90 là đúng.
– **Khẳng định 2:** Tốc độ bơm lớn nhất tại thời điểm t = 60 (phút).
Từ bảng biến thiên, ta thấy tốc độ bơm đạt giá trị lớn nhất là 1080 tại thời điểm $t = 60$ (phút). Khẳng định này là đúng.
– **Khẳng định 3:** Thể tích nước của bể bơi sau 20 phút bơm là 2000 (lít).
$V\left( 20 \right)=\dfrac{1}{100}\left( 30 \cdot {{20}^{3}}-\dfrac{{{20}^{4}}}{4} \right)=\dfrac{1}{100}\left( 30 \cdot 8000 – \dfrac{160000}{4} \right)=\dfrac{1}{100}\left( 240000-40000 \right)=\dfrac{200000}{100}=2000$ (lít). Khẳng định này là đúng.
– **Khẳng định 4:** Tốc độ bơm nước tại thời điểm t là $f\left( t \right)=90{{t}^{2}}-{{t}^{3}}$.
Theo công thức đã tính ở trên, tốc độ bơm nước là $f(t)=\dfrac{1}{100}\left( 90{{t}^{2}}-{{t}^{3}} \right)$. Do đó, khẳng định $f\left( t \right)=90{{t}^{2}}-{{t}^{3}}$ là sai vì thiếu hệ số $\dfrac{1}{100}$.
(Đúng) Tốc độ bơm giảm từ phút thứ 70 đến phút thứ 90.
(Vì): Dựa vào bảng biến thiên của hàm số $f'(t)$ (như trong lời giải), ta thấy tốc độ bơm giảm từ phút thứ 60 đến phút thứ 90. Do đó, tốc độ bơm giảm từ phút thứ 70 đến phút thứ 90 là đúng.
(Đúng) Tốc độ bơm lớn nhất tại thời điểm t = 60 ( phút).
(Vì): Dựa vào bảng biến thiên của hàm số $f(t)$ (như trong lời giải), ta thấy tốc độ bơm đạt giá trị lớn nhất tại thời điểm $t = 60$ (phút) với $f(60) = 1080$.
(Đúng) Thể tích nước của bể bơi sau 20 phút bơm là 2000 (lít).
(Vì): Ta có: $V\left( 20 \right)=\dfrac{1}{100}\left( 30 \cdot {{20}^{3}}-\dfrac{{{20}^{4}}}{4} \right)=\dfrac{1}{100}\left( 30 \cdot 8000 – \dfrac{160000}{4} \right)=\dfrac{1}{100}\left( 240000-40000 \right)=\dfrac{200000}{100}=2000$.
(Sai) Tốc độ bơm nước tại thời điểm t là $f\left( t \right)=100\left( 90{{t}^{2}}-{{t}^{3}} \right)$.
(Vì): Theo công thức đạo hàm, tốc độ bơm nước là $f(t)=V'(t)=\dfrac{1}{100}\left( 90{{t}^{2}}-{{t}^{3}} \right)$. Do đó, $f(t)=100\left( 90{{t}^{2}}-{{t}^{3}} \right)$ là sai.
