Kết quả tìm kiếm cho: ty so

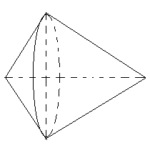
Câu hỏi: Một sợi dây (không co giãn) được quấn đối xứng đúng 10 vòng quanh một ống trụ tròn đều có bán kính \(R = \frac{2}{\pi} ,cm \) (như hình vẽ). Biết rằng sợi dây có chiều dài 50 cm. Hãy tính diện tích xung quanh của ống trụ đó. A. 80cm2 B. 100cm2 C. 60cm2 D. 120cm2 Lời Giải: Đây là các bài toán tính toán S, V về Mặt trụ, Hình trụ, Khối trụ trong Phần Mặt … [Đọc thêm...] vềMột sợi dây (không co giãn) được quấn đối xứng đúng 10 vòng quanh một ống trụ tròn đều có bán kính \(R = \frac{2}{\pi} ,cm \) (như hình vẽ). Biết rằng sợi dây có chiều dài 50 cm. Hãy tính diện tích xung quanh của ống trụ đó.

Câu hỏi: Cho đường thẳng \({d_2}\) cố định, đường thẳng \({d_1}\) song song và cách \({d_2}\) một khoảng cách không đổi. Khi \({d_1}\) quay quanh \({d_2}\) ta được A. Hình tròn B. Khối trụ C. Hình trụ D. Mặt trụ Lời Giải: Đây là các bài toán tính toán S, V về Mặt trụ, Hình trụ, Khối trụ trong Phần Mặt tròn xoay. Theo lý thuyết mặt tròn xoay, khi quay \({d_1}\) … [Đọc thêm...] vềCho đường thẳng \({d_2}\) cố định, đường thẳng \({d_1}\) song song và cách \({d_2}\) một khoảng cách không đổi. Khi \({d_1}\) quay quanh \({d_2}\) ta được

Câu hỏi: Cho lăng trụ \(ABC.A'B'C',\) đáy \(ABC\) là tam giác có \(AB=5,AC=8\) và góc \(\widehat{\left( AB,AC \right)}={{60}^{0}}.\) Gọi \(V,V'\) lần lượt là thể tích của khối lăng trụ ngoại tiếp và nội tiếp khối lăng trụ đã cho. Tính tỉ số \(\frac{V'}{V}?\) A. \(\frac{9}{49}\) B. \(\frac{9}{4}\) C. \(\frac{19}{49}\) D. \(\frac{29}{49}\) … [Đọc thêm...] vềCho lăng trụ \(ABC.A'B'C',\) đáy \(ABC\) là tam giác có \(AB=5,AC=8\) và góc \(\widehat{\left( AB,AC \right)}={{60}^{0}}.\) Gọi \(V,V'\) lần lượt là thể tích của khối lăng trụ ngoại tiếp và nội tiếp khối lăng trụ đã cho. Tính tỉ số \(\frac{V'}{V}?\)

Câu hỏi: Cho một khối trụ có bán kính đáy \(R=a\) và chiều cao \(h=2a\). Mặt phẳng \((P)\) song song với trục \(OO'\) của khối trụ chia khối trụ thành 2 phần, gọi \({{V}_{1}}\) là thể tích phần khối trụ chứa trục \(OO'\), \({{V}_{2}}\) là thể tích phần còn lại của khối trụ. Tính tỉ số \(\frac{{{V}_{1}}}{{{V}_{2}}}\), biết rằng \((P)\) cách \(OO'\) một khoảng … [Đọc thêm...] vềCho một khối trụ có bán kính đáy \(R=a\) và chiều cao \(h=2a\). Mặt phẳng \((P)\) song song với trục \(OO'\) của khối trụ chia khối trụ thành 2 phần, gọi \({{V}_{1}}\) là thể tích phần khối trụ chứa trục \(OO'\), \({{V}_{2}}\) là thể tích phần còn lại của khối trụ. Tính tỉ số \(\frac{{{V}_{1}}}{{{V}_{2}}}\), biết rằng \((P)\) cách \(OO'\) một khoảng bằng \(\frac{a\sqrt{2}}{2}\).

Câu hỏi: Cho \(AA'B'B\) là thiết diện song song với trục OO’ của hình trụ (A, B thuộc đường tròn tâm O). Cho biết \(AB=4,\text{AA }\!\!'\!\!\text{ =3}\) và thể tích của hình trụ bằng \(V=24\pi .\) Khoảng cách d từ O đến mặt phẳng \(\left( \text{AA}'B'B \right)\) là: A. \(d=1\) B. \(d=2\) C. \(d=3\) D. \(d=4\) Lời Giải: Đây là các bài … [Đọc thêm...] vềCho \(AA'B'B\) là thiết diện song song với trục OO’ của hình trụ (A, B thuộc đường tròn tâm O). Cho biết \(AB=4,\text{AA }\!\!'\!\!\text{ =3}\) và thể tích của hình trụ bằng \(V=24\pi .\) Khoảng cách d từ O đến mặt phẳng \(\left( \text{AA}'B'B \right)\) là:

Câu hỏi: Trong số các hình trụ có diện tích toàn phần đều bằng \(S\) thì bán kính \(R\) và chiều cao \(h\) của khối trụ có thể tích lớn nhất là: A. \(R=\sqrt{\frac{S}{2\pi }}\,;\,h=\frac{1}{2}\sqrt{\frac{S}{2\pi }}\). B. \(R=\sqrt{\frac{S}{4\pi }}\,;\,h=\sqrt{\frac{S}{4\pi }}\). C. \(R=\sqrt{\frac{2S}{3\pi }}\,;\,h=4\sqrt{\frac{2S}{3\pi }}\). D. … [Đọc thêm...] vềTrong số các hình trụ có diện tích toàn phần đều bằng \(S\) thì bán kính \(R\) và chiều cao \(h\) của khối trụ có thể tích lớn nhất là:

Câu hỏi: Cho hình lập phương có cạnh bằng a và một hình trụ có hai đáy là hai hình tròn nội tiếp hai mặt đối diện của hình lập phương. Gọi S1 là diện tích 6 mặt của hình lập phương, S2 là diện tích xung quanh của hình trụ. Tỉ số \( \frac{{{S_2}}}{{{S_1}}}\) bằng: A. \( \frac{\pi }{6}\) B. \( \frac{\pi }{2}\) C. \( \frac{1 }{6}\) D. \( \frac{1 }{2}\) Lời Giải: … [Đọc thêm...] vềCho hình lập phương có cạnh bằng a và một hình trụ có hai đáy là hai hình tròn nội tiếp hai mặt đối diện của hình lập phương. Gọi S1 là diện tích 6 mặt của hình lập phương, S2 là diện tích xung quanh của hình trụ. Tỉ số \( \frac{{{S_2}}}{{{S_1}}}\) bằng: