Một vật chuyển động trong 3 giờ với vận tốc $v$ (km/h) phụ thuộc vào thời gian $t$ (h), có đồ thị vận tốc như hình bên dưới. Trong khoảng thời gian 1 giờ kể từ khi bắt đầu chuyển động, đồ thị đó là một phần của đồ thị parabol có đỉnh $I(2;22)$, khoảng thời gian còn lại của đồ thị là một đoạn thẳng song song với trục hoành. Tính quãng đường $S$ (km) mà vật di chuyển được trong 3 giờ đó? 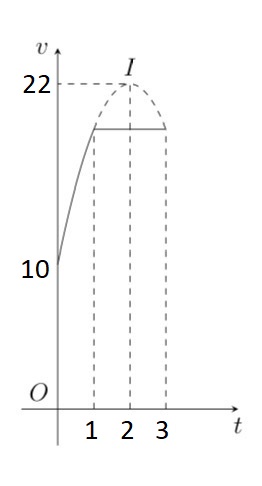
Lời giải
Đáp án: $53$ Gọi phương trình chuyển động của vật trong 1 giờ đầu là: $v(t)=a{{t}^{2}}+bt+c.$ Từ đồ thị, ta có: $\left\{ \begin{align} & v(0)=10 \\ & \\ & v(2)=22 \\ & -\frac{b}{2a}=2 \\ \end{align} \right.$$\Leftrightarrow \left\{ \begin{align} & c=10 \\ & 4a+2b+c=22 \\ & 4a+b=0 \\ \end{align} \right.$$\Leftrightarrow \left\{ \begin{align} & a=-3 \\ & b=12 \\ & c=10 \\ \end{align} \right.$ Suy ra: $v(t)=-3{{t}^{2}}+12t+10$. Quãng đường đi được trong giờ đầu là: ${{S}_{1}}=\int\limits_{0}^{1}{(}-3{{t}^{2}}+12t+10)dt=15$ (km). Tại thời điểm $t=1$, vận tốc của vật là: $v(1)=19$(km/h). Quãng đường vật đi được trong 2 giờ tiếp theo là: ${{S}_{2}}=19.2=38$ (km). Quãng đường vật đi được trong 3 giờ là: $S={{S}_{1}}+{{S}_{2}}=53$ (km).
Một vật chuyển động trong 3 giờ với vận tốc $v$ (km/h) phụ thuộc vào thời gian $t$ (h), có đồ thị vận tốc như hình bên dưới
Ngày Thuộc chủ đề:Trắc nghiệm Ứng dụng Tích phân
