Một nhà sản xuất trung bình bán được 1000 ti vi màn hình phẳng mỗi tuần với giá 14 triệu đồng một chiếc

Một nhà sản xuất trung bình bán được 1000 ti vi màn hình phẳng mỗi tuần với giá 14 triệu đồng một chiếc. Một cuộc khảo sát thị trường chỉ ra rằng nếu cứ giảm giá bán 500 nghìn đồng, số lượng ti vi bán ra sẽ tăng thêm khoảng 100 ti vi mỗi tuần.

a) Gọi $p$ (triệu đồng) là giá của mỗi ti vi, $x$ là số ti vi. Vậy hàm cầu là: $p\left( x \right)=-\dfrac{1}{200}x+20$
.

b) Công ty giảm giá $4,5$ (triệu đồng)/1 tivi cho người mua thì doanh thu của công ty là lớn nhất
.

c) Nếu hàm chi phí hằng tuần là $C\left( x \right)=12000-3x$ (triệu đồng), trong đó $x$ là số ti vi bán ra trong tuần, vậy có $2300$ ti vi được bán ra thì lợi nhuận là cao nhất.
.

d) Nếu hàm chi phí hằng tuần là $C\left( x \right)=12000-3x$ (triệu đồng), trong đó $x$ là số ti vi bán ra trong tuần, nhà sản xuất nên đặt giá bán 8,5 triệu đồng/1 ti vi để lợi nhuận là lớn nhất
.

Lời giải: 2
(Sai) Gọi $p$ (triệu đồng) là giá của mỗi ti vi, $x$ là số ti vi. Vậy hàm cầu là: $p\left( x \right)=-\dfrac{1}{200}x+20$

(Vì): Đúng: Gọi $p$ (triệu đồng) là giá của mỗi ti vi, $x$ là số ti vi. Khi đó hàm cầu là $p=p\left( x \right)$.
Theo giả thiết, tốc độ thay đổi của $x$ tỉ lệ với tốc độ thay đổi của $p$ nên hàm số $p=p\left( x \right)$ là hàm số bậc nhất. Do đó, $p\left( x \right)=ax+b$ ($a$ khác $0$).
Giá tiền ${{p}_{1}}=14$ ứng với ${{x}_{1}}=1000$, giá tiền ${{p}_{2}}=13,5$ ứng với ${{x}_{2}}=1000+100=1100$.
Do đó, phương trình đường thẳng $p\left( x \right)=ax+b$ đi qua hai điểm $\left( 1000;14 \right)$ và $\left( 1100;13,5 \right)$.
Ta có hệ phương trình: $\left\{ \begin{array}{*{35}{l}} 14=1000a+b \\ 13,5=1100a+b \end{array}\right.\Leftrightarrow \left\{ \begin{array}{*{35}{l}} a=\dfrac{-1}{200} \\ b=19 \end{array} \right.$ (thỏa mãn) $\Rightarrow p\left( x \right)=-\dfrac{1}{200}x+19$.

(Đúng) Công ty giảm giá $4,5$ (triệu đồng)/1 tivi cho người mua thì doanh thu của công ty là lớn nhất

(Vì): Đúng: Vì $p=\dfrac{-1}{200}x+19\Rightarrow x=-200p+3800$.
Hàm doanh thu từ tiền bán ti vi là: $R\left( p \right)=px=p\left( -200p+3800 \right)=-200{{p}^{2}}+3800p$.
Để doanh thu là lớn nhất thì ta cần tìm $p$ sao cho $R$ đạt giá trị lớn nhất.
Ta có: ${R}’\left( p \right)=-400p+3800$; ${R}’\left( p \right)=0\Leftrightarrow p=\dfrac{19}{2}$.
Bảng biến thiên:

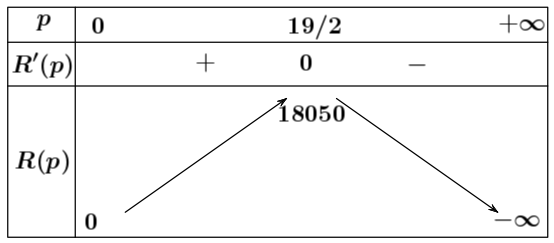
Vậy công ty nên giảm giá số tiền một chiếc ti vi là: $14-\dfrac{19}{2}=4,5$ (triệu đồng) thì doanh thu là lớn nhất.

(Sai) Nếu hàm chi phí hằng tuần là $C\left( x \right)=12000-3x$ (triệu đồng), trong đó $x$ là số ti vi bán ra trong tuần, vậy có $2300$ ti vi được bán ra thì lợi nhuận là cao nhất.

(Vì): Sai: Doanh thu bán hàng của $x$ sản phẩm là: $R\left( x \right)=x.p\left( x \right)=x.\left( \dfrac{-1}{200}x+19 \right)=\dfrac{-{{x}^{2}}}{200}+19x$ (triệu đồng). Do đó, hàm số thể hiện lợi nhuận thu được khi bán $x$ sản phẩm là:
$P\left( x \right)=R\left( x \right)-C\left( x \right)=\dfrac{-{{x}^{2}}}{200}+19x-\left(12000-3x\right)=\dfrac{-{{x}^{2}}}{200}+22x-12000$ (triệu đồng).
Để lợi nhuận là lớn nhất thì $P\left( x \right)$ là lớn nhất. Ta có: ${P}’\left( x \right)=\dfrac{-x}{100}+22$; ${P}’\left( x \right)=0\Leftrightarrow x=2200$.
Bảng biến thiên:

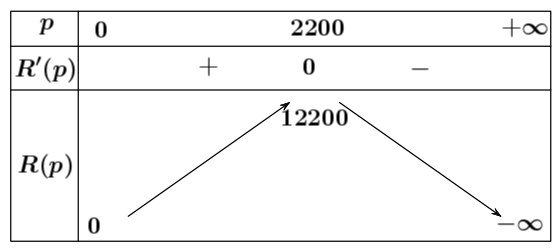
Vậy có $2200$ ti vi được bán ra thì lợi nhuận là cao nhất.
Số ti vi mua tăng lên là: $2200-1000=1200$ (chiếc).

(Sai) Nếu hàm chi phí hằng tuần là $C\left( x \right)=12000-3x$ (triệu đồng), trong đó $x$ là số ti vi bán ra trong tuần, nhà sản xuất nên đặt giá bán 8,5 triệu đồng/1 ti vi để lợi nhuận là lớn nhất

(Vì): Sai: Vậy cửa hàng nên đặt giá bán là: $14-0,5\cdot \dfrac{1200}{100}=8$ (triệu đồng)