Một người nông dân có $15.000.000$ đồng muốn làm một cái hàng rào hình chữ $E$ dọc theo một con sông (như hình vẽ) để làm một khu đất có hai phần chữ nhật để trồng rau

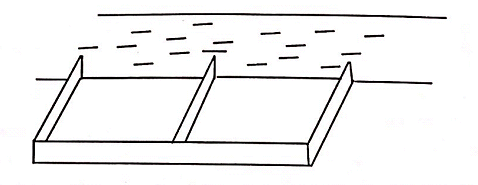
Một người nông dân có $15.000.000$ đồng muốn làm một cái hàng rào hình chữ $E$ dọc theo một con sông (như hình vẽ) để làm một khu đất có hai phần chữ nhật để trồng rau. Đối với mặt hàng rào song song với bờ sông thì chi phí nguyên vật liệu là $60000$ đồng một mét, còn đối với ba mặt hàng rào song song nhau thì chi phí nguyên vật liệu là $50000$ đồng một mét. Gọi $x$ là chiều dài $1$ mặt hàng rào hình chữ $E$ (trong ba mặt song song, $x{>}0$ ). Gọi $y$ là chiều dài mặt hàng rào hình chữ E song song với bờ sông ( $y{>}0$ ).

a) Số tiền phải làm là: $x.3.50000+y.60000=15000000$ đồng.

b) Diện tích đất: $S=x.y=x.\dfrac{500-5x}{2}=250x-\dfrac{3}{2}{{x}^{2}}$.

c) Diện tích lớn nhất của đất rào thu được $\max\limits_{\left( 0;+\infty \right)}{\mathop{\max S}}=6000\left( {{\text{m}}^{2}} \right)$.

d) Diện tích lớn nhất của đất rào thu được khi chiều dài $1$ mặt hàng rào hình chữ $E$ là $50\text{m}$.

Lời giải: (a) Sai: Số tiền phải làm là: $x.3.50000+y.60000=15.000.000\Leftrightarrow y=\dfrac{500-5x}{2}$.
(b) Đúng: Diện tích đất: $S=x.y=x.\dfrac{500-5x}{2}=250x-\dfrac{5}{2}{{x}^{2}}$
(c) Đúng: Ta có: ${S}’=250-5x$; ${S}’=0\Leftrightarrow 250-5x\Leftrightarrow x=50.$
Bảng biến thiên:

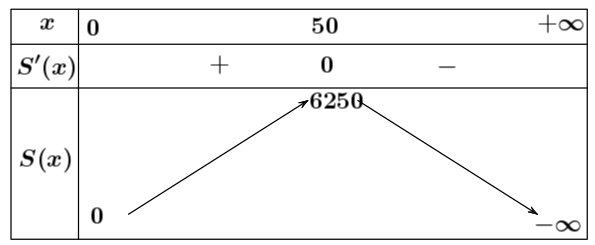
(d) Đúng: Từ bảng biến thiên có $\lim\limits_{\left( 0;+\infty \right)}{\mathop{\max S}}=6250\left( {{\text{m}}^{2}} \right)$ khi $x=50.$
(Đúng) Số tiền phải làm là: $x.3.50000+y.60000=15000000$ đồng.
(Vì): Số tiền phải làm là: $x.3.50000+y.60000=15.000.000\Leftrightarrow y=\dfrac{500-5x}{2}$.
(Sai) Diện tích đất: $S=x.y=x.\dfrac{500-5x}{2}=250x-\dfrac{3}{2}{{x}^{2}}$.
(Vì): Diện tích đất: $S=x.y=x.\dfrac{500-5x}{2}=250x-\dfrac{5}{2}{{x}^{2}}$.
(Sai) Diện tích lớn nhất của đất rào thu được $\max\limits_{\left( 0;+\infty \right)}{\mathop{\max S}}=6000\left( {{\text{m}}^{2}} \right)$.
(Vì): Từ bảng biến thiên có $\lim\limits_{\left( 0;+\infty \right)}{\mathop{\max S}}=6250\left( {{\text{m}}^{2}} \right)$ khi $x=50.$
(Đúng) Diện tích lớn nhất của đất rào thu được khi chiều dài $1$ mặt hàng rào hình chữ $E$ là $50\text{m}$.
(Vì): Ta có: ${S}’=250-5x$; ${S}’=0\Leftrightarrow 250-5x\Leftrightarrow x=50.$