Một bể nước hình nón tròn xoay như hình vẽ có chiều cao 10 m và bán kính đáy 4 mét được đổ nước đến độ cao 8 mét

Một bể nước hình nón tròn xoay như hình vẽ có chiều cao 10 m và bán kính đáy 4 mét được đổ nước đến độ cao 8 mét. Công để bơm hết nước ra từ một vòi ở đỉnh bể được tính theo công thức ${{W}=9,8 . \int_2^{10} x . S(x) . {d} x}$ (đơn vị kilôJun), trong đó ${S(x)\left(m^2\right)}$ là diện tích của lớp nước cách mặt bể ${x(m)}$. Tính ${{W}({kJ})}$ (kết quả làm tròn đến hàng đơn vị).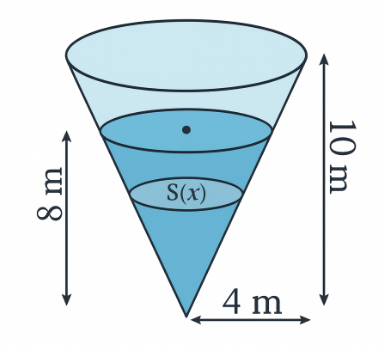
Lời giải Trả lời: 3363. Để tính được công để bơm hết nước ra thì ta cần đi tìm được hàm ${S(x)}$. Lớp nước cách mặt bể là một hình tròn song song và cách mặt bể ${x({~m})}$. Giả sử lớp nước hình tròn đó có bán kính là ${r({~m})}$. Ta gắn trục tọa độ như hình sau. 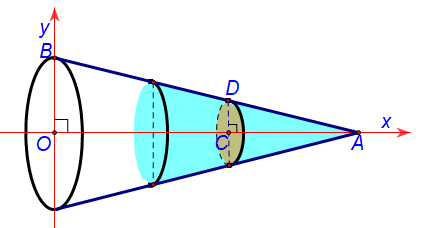Từ giả thiết, ta có $OC=x(~m)\Rightarrow AC=10-x(~m);OA=10(m);OB=4(~m)$. Vì mặt nước cách bể song song với mặt bể nên ${C D / / O B}$. Khi đó, ta áp dụng hệ quả của định lý Talet trong tam giác ${O A B}$, ta có $\frac{AC}{OA}=\frac{CD}{OB}\Leftrightarrow \frac{10-x}{10}=\frac{r}{4}\Leftrightarrow r=\frac{4(10-x)}{10}=\frac{20-2x}{5}$ Suy ra ${S(x)=\pi r^2=\pi\left(\frac{20-2 x}{5}\right)^2}$ Vậy $W=9,8\cdot \int_{2}^{10}{x}\cdot \pi {{\left( \frac{20-2x}{5} \right)}^{2}}~dx\approx 3363(~kJ).$${}$