Khuôn viên của một công viên có dạng hình chữ nhật $ABCD$ với $AB=100\ m;\ AD=80\ m

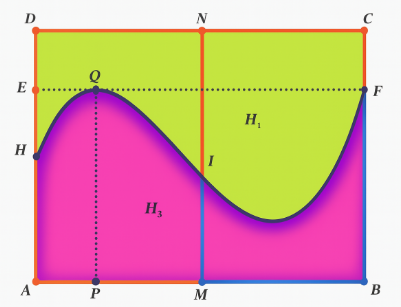
Khuôn viên của một công viên có dạng hình chữ nhật $ABCD$ với $AB=100\ m;\ AD=80\ m.$ Người ta muốn chia công viên thành hai khu, một khu dành cho trẻ em, một khu dành cho người lớn. Để tạo thiết kế độc đáo và lạ mắt, người ta dùng một đường cong chia khuôn viên thành hai phần ${{H}_{1}}$ (không tô màu) dành cho trẻ em và ${{H}_{2}}$ (tô màu) dành cho người lớn như hình vẽ bên với $AH=40\ m;\ AE=60\ m;AP=20\ m$ và $EF//AB;\ PQ//AD$.

Biết rằng khi xét trong một hệ tọa độ $Oxy,$ đường cong trong hình là một phần của đồ thị hàm số bậc ba. Phần chính giữa công viên người ta muốn mắc dây đèn trang trí dọc đoạn thẳng $MN$ như hình. Biết giá tiền mỗi mét dây trang trí của phần dành cho trẻ em là 140 nghìn đồng và phần dành cho người lớn là 180 nghìn đồng. Tổng số tiền mắc dây đèn trang trí trên đoạn $MN$ là bao nhiêu triệu đồng.

Lời giải

Đáp án: $13,9$.

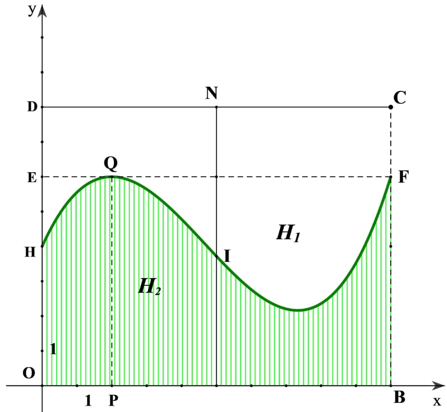
Xét trục tọa độ $Oxy,$ với gốc tọa độ là điểm $A$. Tia $Ox$ trùng với tia $AB$, tia $Oy$ trùng với tia $AD$ thì đường cong ranh giới giữa hai khu vực là đồ thị hàm số bậc ba $y=a{{x}^{3}}+b{{x}^{2}}+cx+d$.

Theo giả thiết đồ thị hàm số này đi qua các điểm $H(0;40);$ $Q(20;60);$ $F(100;60)$ và có điểm cực trị là $Q(20;60)$ nên ta có hệ

$\left\{ \begin{array}{l}

d=40 \\

60=8000a+400b+20c+d \\

60=1000000a+10000b+100c+d \\

3.10000a+2.100b+c=0 \\

\end{array} \right.$

Giải hệ trên ta được $a=\dfrac{1}{10000};\ b=\dfrac{-11}{500};\ c=\dfrac{7}{5};\ d=40$.

Do $M$ là trung điểm của $AB$ nên tọa độ điểm $I$ là $(50;67,5).$ Do đó chiều dài đoạn dây thuộc phần dành cho người lớn là $67,5m$, chiều dài đoạn dây thuộc phần dành cho trẻ em là $12,5m$.

Tổng số tiền mắc dây đèn là $67,5.0,18+12,5.0,14=13,9$ (triệu đồng).