GIẢI CHI TIẾT SÁCH BÀI TẬP toán lớp 8 Bài tập cuối chương 5 – Sách Cánh diều
================
Giải SBT Toán 8 Bài tập cuối chương 5 trang 103
Bài 37 trang 103 SBT Toán 8 Tập 1 : Cho hình bình hànhcó. Số đo các góc của hình bình hànhlà:
A..
B. .
C. .
D..
Lời giải:
Xét hình bình hành , ta có:
Mà nên
Suy ra
→ Đáp án đúng là đáp án C.
Bài 38 trang 103 SBT Toán 8 Tập 1 : Cho hình vuôngcó độ dài bằng 8 cm. Độ dài đường chéolà:
A.
B.
C.
D.
Lời giải:
Xét tam giác vuông cânta có:
suy ra
Vậy độ dài đường chéo
→ Đáp án đúng là đáp án B.
Bài 39 trang 103 SBT Toán 8 Tập 1 : Cho tứ giáccólần lượt là trung điểm của. Điều kiện của tứ giácđể tứ giáclà hình chữ nhật là:
A.
B.
C.
D.
Lời giải:
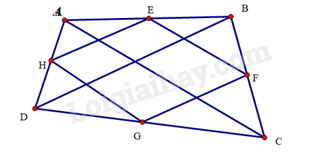
Nối
Xét tam giáccólần lượt là trung điểm củanênlà đường trung bình của tam giác.
Suy ra(1)
Tương tự xét tam giáccólần lượt là trung điểm củanênlà đường trung bình của tam giácsuy ra(2)
Từ (1), (2) suy ranênlà hình bình hành (dấu hiệu nhận biết).
Để hình bình hànhlà hình chữ nhật thìhay
Lại có(dolà đường trung bình của tam giác) nênmà(cmt) nên.
Vậy tứ giáccần cóthìlà hình chữ nhật.
→ Đáp án đúng là đáp án C.
Bài 40 trang 103 SBT Toán 8 Tập 1 : Một công ti dự định làm một đường ống dẫn từ một nhà máu ở địa điểmtrên bờ đến một địa điểmtrên biển. Khoảng cách giữa địa điểmtrên đảo với địa điểm, địa điểmlần lượt là,;vuông góc với(minh họa ở Hình 27). Giá làm 1 km đường ống là 5 000 đô la Mỹ. Hỏi chi phí làm đường ống từ địa điểmđến địa điểmlà bao nhiêu đồng? Biết 1 đô la Mỹ bằng 23 635 đồng.
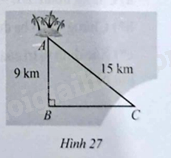
Lời giải:
Trong tam giácvuông tạita có:(theo định lí Pythagore).
Suy ra. Do đó
Chi phí làm đường ống từ địa điểmđến địa điểmlà:
(đồng)
Bài 41 trang 104 SBT Toán 8 Tập 1 : Cho tam giácvuông tạicó đường cao. Kẻvuông góc vớitạivàvuông góc vớitại. Trên tialấy điểmsao cho. Trên tialấy điểmsao cho.
a) Chứng minhlà trung điểm của.
b) Tứ giáclà hình gì? Vì sao?
c) Chứng minh.
Lời giải:
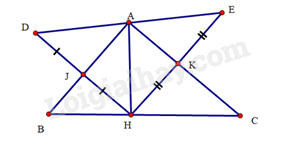
a) Xétvuông tạivàvuông tạicó:
(gt),là cạnh chung
Do đó(hai cạnh góc vuông)
Suy ra(hai cạnh tương ứng) và(hai góc tương ứng)
Tương tự ta cũng chứng minh được(hai cạnh góc vuông)
Suy ra(hai cạnh tương ứng) và(hai góc tương ứng)
Ta có:
Haynên ba điểmthẳng hàng
Lại cóvànên
Do đólà trung điểm của.
b) Ta cótạinên
tạinên
Xét tứ giáccó:
nên là hình chữ nhật.
c) Xét tam giácvuông tạivà tam giácvuông tạicó:
(gt),là cạnh chung
Do đó(hai cạnh góc vuông)
Suy ra(hai cạnh tương ứng)
Tương tự, ta cũng có(hai cạnh góc vuông)
Suy ra(hai cạnh tương iwnsg)
Khi đó
Vậy.
Bài 42 trang 104 SBT Toán 8 Tập 1 : Cho hình thang câncó. Kẻvuông góc vớitại. Lấy điểmthuộc cạnhsao cho.
a) Chứng minh tứ giáclà hình bình hành.
b) Đường thẳng quanullsong song vớicắttại. Tứ giáclà hình gì? Vì sao?
c) Tìm điều kiện của hình thang cânđểlà trung điểm của(bỏ qua giả thiết).
Lời giải:
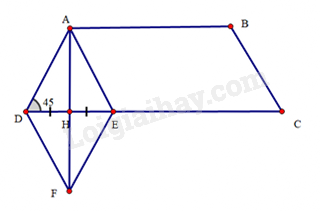
a) (cạnh góc vuông – cạnh góc vuông), suy ra(hai cạnh tương ứng)
Xét tứ giác, ta có:
Vìmànên
Vậy tứ giáclà hình bình hành.
b) Xét tam giácvà, ta có:
(so le trong);;
Suy ra(g.c.g)
Suy ra
Xét tứ giác, ta có:
Mà
Suy ra tứ giáclà hình thoi.
c) Đểlà trung điểm củathìvà ba điểmthẳng hàng.
Khi bỏ qua giả thiếtthì ta chứng minh được tứ giáccó hai đường chéo cắt nhau tại trung điểm của mỗi đường nênlà hình bình hành.
Dovàđều là hình bình hành nênvà
Suy ravà
Tứ giáccóvànênlà hình bình hành.
Màlà trung điểm của, suy ralà trung điểm củahay.
Mặt khác,(vìlà hình bình hành), suy ra
Dễ thấy nếu hình thang câncóthìlà trung điểm của.
Vậy điều kiện của hình thang cânđểlà trung điểm củalà.
Bài 43 trang 104 SBT Toán 8 Tập 1 : Cho hình bình hànhcó. Gọilần lượt là trung điểm của
a) Chứng minh tứ giáclà hình bình hành.
b) Gọilà giao điểm củavàlà giao điểm củavà. Chứng minh tứ giáclà hình chữ nhật.
c) Tìm điều kiện của hình bình hànhđể tứ giáclà hình vuông.
d) Tính diện tích của tứ giác, biết.
Lời giải:
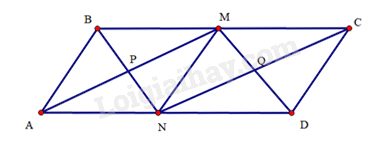
a) Dolà hình bình hành nênvà
Mànên
Lại cólần lượt là trung điểm củanên
Do đó
Tứ goáccóvànên là hình bình hành.
b) Tương tự câu a, ta chứng minh đượclà hình bình hành.
Dođều là hình bình hành nên. Suy ra tứ giáclà hình bình hành.
(c.g.c). Suy ra.
Tứ giáccónênlà hình thoi. Suy ra
Hình bình hànhcónênlà hình chữ nhật.
c) Để hình chữ nhậtlà hình vuông thì.
Màlà hình thoi nênlà hình bình hành. Suy racắt nhau tại trung điểmcủa mỗi đường. mà, suy ra
Hình bình hànhcónênlà hình chữ nhật
Suy rahay
Hình bình hànhcónênlà hình chữ nhật.
Dễ thấy, nếu hình bình hànhlà hình chữ nhật vàthìlà hình vuông.
Vậy điều kiện của hình bình hànhđểlà hình vuông là hình bình hànhlà hình chữ nhật có.
d) Ta có:nên
Dolà hình thoi nênlà tia phân giác của
Suy ra
Tam giáccóvànên tam giácđều.
Suy ra
Dolà trung điểm củanên
Trong tam giácvuông tại, ta có:
Suy ra. Do đócm
Dolà hình chữ nhật nên diện tích củalà:
.
Bài 44 trang 104 SBT Toán 8 Tập 1 : Cho hình vuông. Lấy điểmthuộc đường chéo. Kẻvuông góc vớitại,vuông góc vớitại.
a) Chứng minh:.
b) Chứng minh ba đường thẳngcùng đi qua một điểm.
c) Xác định vị trí của điểmtrên đường chéođể diện tích của tứ giáclớn nhất.
Lời giải:
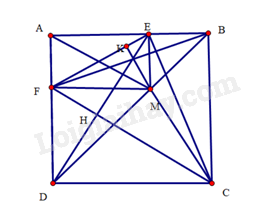
Gọilà giao điểm củavà,là giao điểm củavà.
Dolà hình vuông nên ta có:
a) Ta chứng minh được tam giácvuông cân tại.
Suy ra
Tứ giáccónênlà hình chữ nhật. Suy ra.
Do đó(vì cùng bằng)
(c.g.c). Suy ra,.
Trong tam giácvuông tại, ta có:
Suy rahay. Từ đó ta tính được. Vậy.
b) Tương tự câu a, ta chứng minh được.
(c.g.c). Suy ra. Mà(vìlà hình chữ nhật) suy ra.
(c.c.c). Suy rahay
Trong tam giácvuông tại, ta có
Suy rahay. Từ đó, ta tính được. Do đó,.
Trong tam giác, ta có:nên ba đường thẳnglà các đường cao của tam giác. Vậy ba đường thẳngcùng đi qua một điểm.
c) Chu vi của hình chữ nhậtlà:
Màkhông đổi nên chu vi của hình chữ nhậtkhông đổi. Do đó, diện tích của tứ giáclớn nhất khilà hình vuông. Suy ra.
Khi đó(cạnh góc vuông – góc nhọn kề). Suy rahaylà trung điểm của
Vậy vớilà trung điểm củathì diện tích của tứ giáclớn nhất.
=============
THUỘC: GIẢI SÁCH BÀI TẬP MÔN TOÁN LỚP 8 – Cánh diều
