Giải SBT (Cánh diều) Toán 8 Bài 7: Hình vuông

GIẢI CHI TIẾT SÁCH BÀI TẬP toán lớp 8 Bài 7: Hình vuông – Sách Cánh diều

================

Giải SBT Toán 8 Bài 7: Hình vuông

Bài 31 trang 102 SBT Toán 8 Tập 1 : Cho hình vuông$ABCD$có hai đường chéo$AC$và$BD$cắt nhau tại$O$. Trên tia đối của tia$CB$lấy điểm$K$sao cho$BC=CK$. Từ điểm$B$kẻ đường thẳng song song với$AC$cắt tia$DC$tại$E$. Gọi$F$là trung điểm của$BE$.

a) Chứng minh các tứ giác$BOCF$và$BDKE$đều là hình vuông.

b) Tứ giác$CDOF$có thể là hình vuông không? Vì sao?

Lời giải:

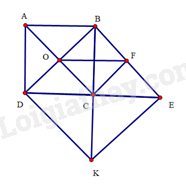
a) Tứ giác$ABCD$là hình vuông suy ra$\widehat{ACB}={45}^{\circ },OB=OC,\widehat{BOC}=\widehat{DOC}={90}^{\circ }$.

Ta có:$\widehat{BOF}=\widehat{DOC}$(hai góc đồng vị) nên$\widehat{OBF}={90}^{\circ };\widehat{CBE}=\widehat{ACB}$(hai góc so le trong) nên$\widehat{CBE}={45}^{\circ }$.

Từ đó ta chứng minh được tam giác$BDE$vuông cân tại$B$và tam giác$BCE$vuông cân tại$C$. Suy ra$BD=BE$và$BC=EC$.

$\mathrm{\Delta }BCF=\mathrm{\Delta }ECF$(c.c.c). Suy ra ta tính được$\widehat{BFC}=\widehat{EFC}={90}^{\circ }$

Tứ giác$BOCF$có$\widehat{BOC}=\widehat{OBF}=\widehat{BFC}={90}^{\circ }$nên$BOCF$là hình chữ nhật.

Hình chữ nhật$BOCF$có$OB=OC$nên$BOCF$là hình vuông.

Ta có:$BC=CD$và$BC=CE$nên$CD=CE$.

Tứ giác$BDKE$có hai đường chéo$BK$và$DE$cắt nhau tại trung điểm$C$của mỗi đường nên$BDKE$là hình bình hành.

Hình bình hành$BDKE$có$\widehat{DBE}={90}^{\circ }$nên$BDKE$là hình chữ nhật

Hình chữ nhật$BDKE$có$BD=BE$nên$BDKE$là hình vuông

b) Tứ giác$CDOF$có$\widehat{ODC}={45}^{\circ }$nên$CDOF$không thể là hình vuông.

Bài 32 trang 102 SBT Toán 8 Tập 1 : Cho hình chữ nhật$ABCD$có hai cạnh kề không bằng nhau. Tia phân giác của các góc$A$và$B$cắt nhau tại$E$. Tia phân giác của các góc$C$và$D$cắt nhau tại$F$. Gọi$G$là giao điểm của$AE$và$DF$,$H$là giao điểm của$BE$và$CF$. Chứng minh:

a)$GH//CD$

b) Tứ giác$GFHE$là hình vuông

Lời giải:

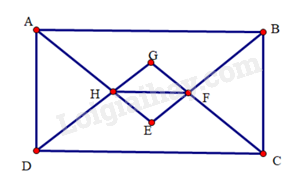
a) Do$ABCD$là hình chữ nhật nên$\widehat{DAB}=\widehat{ABC}=\widehat{BCD}=\widehat{CDA}={90}^{\circ }$

Mà $AE,BE,CF,DF$lần lượt là các tia phân giác của các góc$DAB,ABC,BCD,CDA$

suy ra $\widehat{DAE}=\widehat{EAB}=\widehat{ABE}=\widehat{EBC}=\widehat{BCF}=\widehat{FCD}=\widehat{CDF}=\widehat{FDA}={45}^{\circ }$

Do đó, các tam giác$EAB,FCD,GAD,HBC$đều là tam giác vuông cân.

$\mathrm{\Delta }GAD=\mathrm{\Delta }HBC$(g.c.g). Suy ra$GD=HC$. Mà$FD=FC$, suy ra$FG=FH$.

Do đó, tam giác$FGH$vuông cân tại$F$. Suy ra$\widehat{FGH}={45}^{\circ }$.

Ta có:$\widehat{FGH}=\widehat{CDF}={45}^{\circ }$và$\widehat{FGH},\widehat{CDF}$nằm ở vị trí đồng vị nên$GH//CD$.

b)$\widehat{EGF}=\widehat{AGD}={90}^{\circ }$(hai góc đối đỉnh)

Tứ giác$GFHE$là hình chữ nhật.

Hình chữ nhật$GFHE$có$FG=FH$nên$GFHE$là hình vuông.

Bài 33 trang 102 SBT Toán 8 Tập 1 : Cho hình bình hành$ABCD$. Ở phía ngoài hình bình hành, vẽ các hình vuông$ABEF$và$ADGH$(Hình 26). Chứng minh:

a) $\mathrm{\Delta }AHF=\mathrm{\Delta }ADC$

b) $AC\mathrm{\perp }HF$.

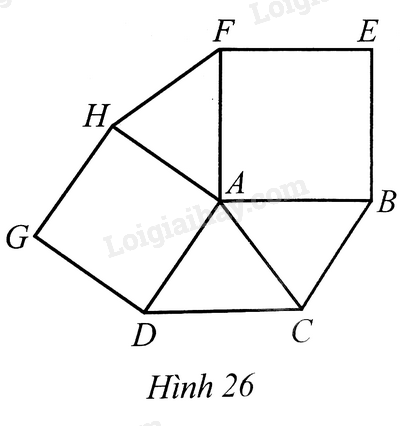
Lời giải:

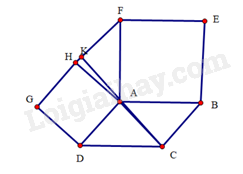
Gọi$K$là giao điểm của$AC$và$HF$

a) Do $ABEF$và$ADGH$đều là hình vuông nên$\widehat{BAF}=\widehat{DAH}={90}^{\circ },AH=BA,AH=DA$

Do$ABCD$là hình bình hành nên$BA=DC$. Suy ra$AF=DC$

Ta chứng minh được$\widehat{HAF}+\widehat{DAB}={180}^{\circ }$và$\widehat{ADC}+\widehat{DAB}={180}^{\circ }$

Suy ra$\widehat{HAF}=\widehat{ADC}$

Xét hai tam giác$HAF$và$ADC$, ta có:$AH=DA,\widehat{HAF}=\widehat{ADC},AF=DA$

Suy ra$\mathrm{\Delta }HAF=\mathrm{\Delta }ADC$(c.g.c)

b) Ta có: $\widehat{HAK}+\widehat{DAH}+\widehat{DAC}=\widehat{CAK}={180}^{\circ }$và$\widehat{DAH}={90}^{\circ }$nên$\widehat{HAK}+\widehat{DAC}={90}^{\circ }$

Mà$\widehat{AHF}=\widehat{DAC}$(vì$\mathrm{\Delta }HAF=\mathrm{\Delta }ADC$), suy ra$\widehat{HAK}+\widehat{AHF}={90}^{\circ }$

Trong tam giác$AHK$, ta có:$\widehat{AKH}+\widehat{HAK}+\widehat{AHF}={180}^{\circ }$. Suy ra$\widehat{AKH}={90}^{\circ }$

Vậy$AK\mathrm{\perp }HK$hai$AC\mathrm{\perp }HF$.

Bài 34 trang 102 SBT Toán 8 Tập 1 : Cho tam giác$ABC$có các đường trung tuyến$BD,CE$cắt nhau tại$G$. Gọi$F,H$lần lượt là trung điểm của$BG,CG$.

a) Tứ giác $EFHD$là hình gì? Vì sao?

b) Tìm điều kiện của tam giác $ABC$để tứ giác$EFHD$là hình vuông.

Lời giải:

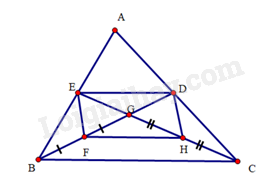
a) Do $G$là trọng tâm tam giác$ABC$nên$DG=\frac{1}{2}BG,EG=\frac{1}{2}CG$. Mà$F,H$lần lượt là trung điểm của$BG,CG$nên$DG=BF=FG,EG=CH=HG$.

Tứ giác$EFHG$có hai đường chéo$EH$và$DF$cắt nhau tại trung điểm của mỗi đường nên$EFHG$là hình bình hành.

b) Để hình bình hành $EFHG$là hình vuông thì$EH=DF$và$EH\mathrm{\perp }DF$

suy ra$BG=CG,EG=DG$và$BD\mathrm{\perp }CE$.

$\mathrm{\Delta }BEG=\mathrm{\Delta }CDG$(c.g.c). Suy ra$BE=CD$. Mà$AB=2BE,AC=2CD$, suy ra$AB=AC$.

Dễ thấy nếu$AB=AC$và$BD\mathrm{\perp }CE$thì tứ giác$EFHG$là hình vuông.

Vậy tam giác$ABC$cân tại$A$có đường trung tuyến$BD$,$CE$vuông góc với nhau thì tứ giác$EFHG$là hình vuông.

Bài 35 trang 103 SBT Toán 8 Tập 1 : Cho hình vuông$ABCD$có$AB=12cm$. Trên cạnh$CD$lấy điểm$E$sao cho$DE=5cm$. Tia phân giác của góc$BAE$cắt$BC$tại$F$. Trên tia đối của tia$BC$lấy điểm$M$sao cho$BM=DE$.

a) Chứng minh $AE=AM=DE$

b) Tính độ dài $BF$.

Lời giải:

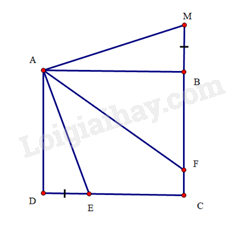
a) $\mathrm{\Delta }ADE=\mathrm{\Delta }ABM$(c.g.c)

Suy ra$AE=AM$và$\widehat{DAE}=\widehat{BAM}$.

Do$AF$là tia phân giác của$\widehat{BAE}$nên$\widehat{EAF}=\widehat{BAF}$.

Suy ra$\widehat{DAE}+\widehat{EAF}=\widehat{BAM}+\widehat{BAF}$hay$\widehat{DAF}=\widehat{MAF}$.

Mà$\widehat{DAF}=\widehat{MFA}$(hai góc so le trong) , suy ra$\widehat{MFA}=\widehat{MAF}$

Do đó, tam giác$MAF$cân tại$M$. Suy ra$AM=FM$

Mà$AE=AM$, suy ra$AE=AM=FM$.

b) Trong tam giác $ADE$vuông tại$D$, ta có:$A{E}^2=A{D}^2+D{E}^2$

Suy ra$AE=13cm$. Mà$FM=AE$, suy ra$FM=13cm$.

Ta có:$FM=BM+BF$. Mà$BM=DE=5cm$và$FM=13cm$, suy ra$BF=8cm$.

Bài 36 trang 103 SBT Toán 8 Tập 1 : Cho hình vuông$ABCD$. Lấy điểm$E$thuộc cạnh$CD$và điểm$F$thuộc tia đối của tia$BC$sao cho$BF=DE$.

a) Chứng minh tam giác $AEF$là tam giác vuông cân

b) Gọi $I$là trung điểm của$EF$. Trên tia đối của tia$IA$lấy điểm$K$sao cho$IK=IA$. Chứng minh tứ giác$AEKF$là hình vuông.

c) Chứng minh $I$thuộc đường thẳng$BD$.

Lời giải:

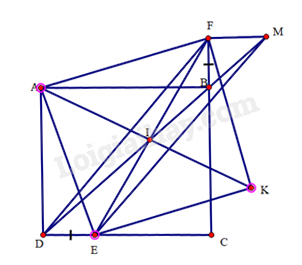
Từ điểm$F$kẻ đường thẳng song song với$CD$cắt đường thẳng$BD$tại$M$

a) $\mathrm{\Delta }ADE=\mathrm{\Delta }ABF$(c.g.c)

Suy ra$AE=AF$và$\widehat{DAE}=\widehat{BAF}$

Suy ra$\widehat{DAE}+\widehat{BAE}=\widehat{BAF}+\widehat{BAE}$hay$\widehat{BAD}=\widehat{EAF}$.

Do đó,$\widehat{EAF}={90}^{\circ }$

Tam giác$AEF$có$\widehat{EAF}={90}^{\circ },AE=AF$nên tam giac$AEF$vuông cân tại$A$.

b) Tứ giác $AEKF$có hai đường chéo$AK,EF$cắt nhau tại trung điểm$I$của mỗi đường nên$AEKF$là hình bình hành

hình bình hành$AEKF$có$\widehat{EAF}={90}^{\circ }$nên$AEKF$là hình chữ nhật.

hình chữ nhật$AEKF$có$AE=AF$nên$AEKF$là hình vuông.

c) Do $ABCD$là hình vuông nên ta tính được$\widehat{CBD}={45}^{\circ }$. Mà$\widehat{FBM}=\widehat{CBD}$(hai góc đối đỉnh), suy ra$\widehat{FBM}={45}^{\circ }$.

Do$MF=CD$nên$\widehat{BFM}=\widehat{BCD}$(cặp góc so le trong)

Do đó$\widehat{BFM}={90}^{\circ }$. Ta chứng minh được tam giácnullvuông cân tại$F$. Suy ra$MF=BF$. Mà$BF=DE$, suy ra$MF=DE$.

Tứ giác DEMFcó$MF=DE$và$MF//DE$ nên DEMFlà hình bình hành.

Mà$I$là trung điểm của$EF$, suy ra$I$là trung điểm của$DM$

Vậy$I$thuộc đường thẳng$DM$hay$I$thuộc đường thẳng$BD$.

=============
THUỘC: GIẢI SÁCH BÀI TẬP MÔN TOÁN LỚP 8 – Cánh diều