Giải SBT (Cánh diều) Toán 8 Bài 3: Hình thang cân - Sách Toán

GIẢI CHI TIẾT SÁCH BÀI TẬP toán lớp 8 Bài 3: Hình thang cân – Sách Cánh diều

================

Giải SBT Toán 8 Bài 3: Hình thang cân

Bài 11 trang 92 SBT Toán 8 Tập 1 : Cho tứ giác $A B C D$ có $\hat{C} = \hat{D}$ và $A D = B C$ . Chứng minh tứ giác $A B C D$ là hình thang cân.

Lời giải:

Sách bài tập Toán 8 Bài 3 (Cánh diều): Hình thang cân (ảnh 1)

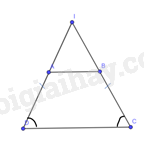
Gọi $I$ là giao điểm của $A D$ và $B C$

Do $\hat{C} = \hat{D}$ nên tam giác $I C D$ cân tại $I$ . Suy ra $I D = I C$

Mà $A D = B C$ , suy ra $I A = I B$ . Do đó, tam giác $I A B$ cân tại $I$ .

Vì hai tam giác $I A B$ và $I C D$ đều cân tại $I$ nên

$\hat{I A B} = \hat{D}$ (cùng bằng $\frac{180^{\circ} -}{\hat{I}}$ )

Mà $\hat{I A B}$ và $\hat{D}$ nằm ở vị trí đồng vị, suy ra $A B / / C D$

Tứ giác $A B C D$ có $A B / / C D$ và $\hat{C} = \hat{D}$ nên $A B C D$ là hình thang cân.

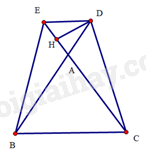
Bài 12 trang 92 SBT Toán 8 Tập 1 : Cho hình thang cân $A B C D$ có $A B / / C D, A B < C D$ , hai đường chéo $A C$ và $B D$ cắt nhau tại $P$ , hai cạnh bên $A D$ và $B C$ kéo dài cắt nhau tại $Q$ . Chứng minh $P Q$ là đường trung trực của hai đáy hình thang cân $A B C D$ .

Lời giải:

Sách bài tập Toán 8 Bài 3 (Cánh diều): Hình thang cân (ảnh 2)

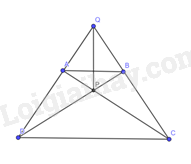
$Δ A C D = Δ B D C$ (c.g.c). Suy ra $\hat{P C D} = \hat{P D C}$

Do đó, tam giác $P C D$ cân tại $P$ . Suy ra $P C = P D$

Mà $A C = B D$ , suy ra $P A = P B$

Do $A B / / C D$ nên $\hat{Q A B} = \hat{A D C}; \hat{Q B A} = \hat{B C D}$ (các cặp góc đồng vị)

Mặt khác, $\hat{A D C} = \hat{B C D}$ nên $\hat{Q A B} = \hat{Q B A}$

Do đó, tam giác $Q A B$ cân tại $Q$ . Suy ra $Q A = Q B$

Mà $A D = B C$ , suy ra $Q D = Q C$

Ta có: $P A = P B, P C = P D$ và $Q A = Q B, Q C = Q D$ nên $P Q$ là đường trung trực của cả hai đoạn thẳng $A B$ và $C D$ .

Bài 13 trang 92 SBT Toán 8 Tập 1 : Cho hình thang cân $A B C D$ có $A B / / C D, A B = 3 m c, C D = 6 c m, A D = 2.5 c m$ . Gọi $M, N$ lần lượt là hình chiếu của $A, B$ trên đường thẳng $C D$ . Tính độ dài các đoạn thẳng $D M, D N, A M$ .

Lời giải:

Sách bài tập Toán 8 Bài 3 (Cánh diều): Hình thang cân (ảnh 3)

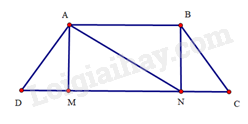
$Δ A D M = Δ B C N$ (cạnh huyền – góc nhọn)

Suy ra $A M = B N; D M = C N$

$Δ A B N = Δ N M A$ (cạnh huyền – góc nhọn)

Suy ra $A B = N M$ . Do đó, $N M = 3 c m$

Ta có: $D M + N M + C N = C D$ và $D M = C N$ nên $2 D M + 3 = 6$

Suy ra $D M = 1, 5$

Mà $D N = D M + N M$ , suy ra $D N = 4, 5 c m$

Trong tam giác $A D M$ vuông tại $M$ , ta có: $A D^{2} = A M^{2} + D M^{2}$

Suy ra $A M^{2} = A D^{2} - D M^{2} = 4$ . Vậy $A M = \sqrt{4} = 2 (c m)$ .

Bài 14 trang 92 SBT Toán 8 Tập 1 : Cho tam giác $A B C$ cân tại $A$ . Lấy điểm $M, N$ lần lượt trên cạnh $A B, A C$ sao cho $A M = A N$ .

a) Chứng minh tứ giác $B M N C$ là hình thang cân

b) Xác định vị trí các điểm $M, N$ để $B M = M N = N C$ .

Lời giải:

Sách bài tập Toán 8 Bài 3 (Cánh diều): Hình thang cân (ảnh 4)

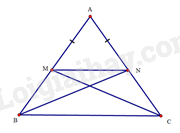
a) Vì hai tam giác $A M N$ và $A B C$ đều cân tại $A$ nên

$\hat{A M N} = \hat{A B C}$ (cùng bằng $\frac{180^{\circ} -}{\hat{A}}$ )

Mà $\hat{A M N}$ và $\hat{A B C}$ nằm ở vị trí đồng vị, suy ra $M N / / B C$ .

Tứ giác $B M N C$ có $M N / / B C$ và $\hat{M B C} = \hat{N C B}$ nên $B M N C$ là hình thang cân.

b) Do $B M = M N$ nên tam giác $M B N$ cân tại $M$ . Suy ra $\hat{M N B} = \hat{M B N}$ . Mà $\hat{M N B} = \hat{N B C}$ (hai góc so le trong), suy ra $\hat{M B N} = \hat{N B C}$ . Do đó, $B N$ là tia phân giác của góc $A B C$ .

Chứng minh tương tự ta được $C M$ là tia phân giác của góc $A C B$ .

Dễ thấy, nếu các điểm $M, N$ được xác định sao cho $B M, C N$ lần lượt là tia phân giác của góc $A B C, A C B$ thì $B N = M N = C N$ .

Vậy $M$ là giao điểm của $A B$ và tia phân giác của góc $A C B, N$ là giao điểm của $A C$ và tia phân giác của góc $A B C$ thì $B N = M N = C N$ .

Bài 15 trang 92 SBT Toán 8 Tập 1 : Cho tam giác đều $A B C$ có độ dài cạnh là 6 cm. trên tia $B A, C A$ lần lượt lấy điểm $D, E$ sao cho $A D = A E = 2 c m$ (Hình 12)

a) Tứ giác $B C D E$ là hình gì? Vì sao?

b) Tính độ dài đoạn thẳng $C D$ (làm tròn kết quả đến hàng phần mười của centimet).

Sách bài tập Toán 8 Bài 3 (Cánh diều): Hình thang cân (ảnh 5)

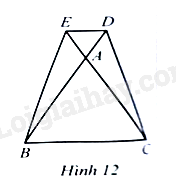
Lời giải:

Sách bài tập Toán 8 Bài 3 (Cánh diều): Hình thang cân (ảnh 6)

a) Tam giác đều $A B C$ có $A B = B C = A C = 6 c m$ ; $\hat{B A C} = \hat{C B A} = \hat{A C B} = 60^{\circ}$

Ta có: $\hat{D A E} = \hat{B A C}$ (hai góc đối đỉnh) nên $\hat{D A E} = 60^{\circ}$

Tam giác $A D E$ có $A D = A E$ và $\hat{D A E} = 60^{\circ}$ nên $A D E$ là tam giác đều. Suy ra $\hat{A D E} = 60^{\circ}$ . Do đó $\hat{C B A} = \hat{A D E}$ (vì cùng bằng $60^{\circ}$ ). Mà $\hat{C B A}$ và $\hat{A D E}$ nằm ở vị trí so le trong, suy ra $B C / / D E$ .

Ta có: $A B = A C$ và $A D = A E$ nên $B D = C E$ .

Tứ giác $B C D E$ có $B C / / D E$ và $B D = C E$ nên $B C D E$ là hình thang cân.

b) Kẻ $D H$ vuông góc với $C E$ tại $H$ .

$Δ A D H = Δ E D H$ (cạnh huyền – cạnh góc vuông)

Suy ra $A H = E H = \frac{A E}{2} = 1 c m$

Trong tam giác $A D H$ vuông tại $H$ , ta có: $C D^{2} = C H^{2} + D H^{2}$ . Suy ra $C D^{2} = 52$

Vậy $C D = \sqrt{52} \approx 7, 2 (c m)$ .

=============
THUỘC: GIẢI SÁCH BÀI TẬP MÔN TOÁN LỚP 8 – Cánh diều

Reader Interactions

Để lại một bình luận Hủy