GIẢI CHI TIẾT SÁCH BÀI TẬP toán lớp 8 Bài 6: Hình thoi – Sách Cánh diều
================
Giải SBT Toán 8 Bài 6: Hình thoi
Bài 26 trang 99 SBT Toán 8 Tập 1 : Cho hình thoicó góctù. Kẻvuông góctại,vuông góc vớitại. Gọilần lượt là giao điểm củavới. Chứng minh tứ giáclà hình thoi.
Lời giải:
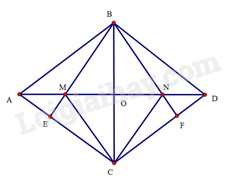
Gọilà giao điểm củavà
Dolà hình thoi nênvuông góc vớitại trung điểmcủa. Suy ralà đường trung trực của. Do đó.
Dolà hình thoi nên.
Suy ra(cạnh huyền – góc nhọn kề)
Do đó. Mà, suy ra.
(cạnh góc vuông – góc nhọn). suy ra
Màvà, suy ra.
Tứ giáccónênlà hình thoi.
Bài 27 trang 99 SBT Toán 8 Tập 1 : Cho một hình thoi có độ dài hai đường chéo làm vàm. Tính chu vi và diện tích của hình thoi đó.
Lời giải:
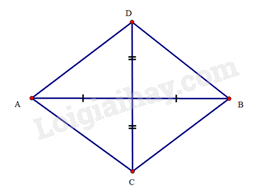
Xét hình thoicó,.
Gọilà giao điểm của hai đường chéovà.
Dolà hình thoi nênlà trung điểm củavà.
Ta tính được:
.
Trong tam giácvuông tại, ta có:. Suy ra
Chu vi của hình thoilà:
Diện tích của hình thoilà:.
Bài 28 trang 100 SBT Toán 8 Tập 1 : Cho tam giácnhọn có các đường cao. Tia phân giác của các góccắt nhau tạivà cắtlần lượt tại. Tiacắttại, tiacắttại. Chứng minh:
a)
b) Tứ giáclà hình thoi.
Lời giải:
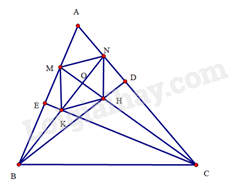
a) Do tam giácvuông tạivà tam giácvuông tạinên. Suy ra.
Màvàlần lượt là tia phân giác củavà, suy ra.
Do tam giácvuông tạinên
Suy rahay.
Do đó ta tính được. Vậy.
b) (cạnh góc vuông – góc nhọn kề). Suy ra
(cạnh góc vuông – góc nhọn kề). Suy ra.
Tứ giáccó hai đường chéovàcắt nhau tại trung điểmcủa mỗi đường nênlà hình bình hành.
Hình bình hànhcónênlà hình thoi.
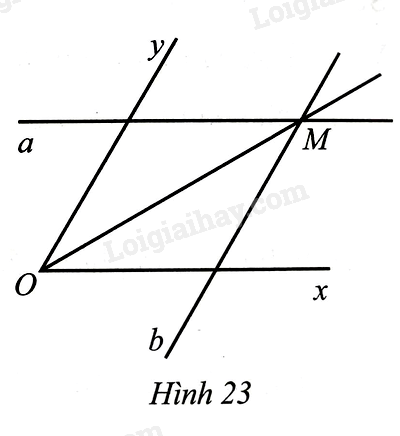
Bài 29 trang 100 SBT Toán 8 Tập 1 : Cho góckhác góc bẹt. Dùng thước hai lề (thước có hai cạnh song song). Đặt thước hai lề sao cho một cạnh của thước trùng với cạnhcủa góc, vẽ đường thẳngtheo cạnh kia của thước. đặt thước hai lề sao cho một cạnh của thước trùng với cạnhcủa góc. Chứng minh tialà tia phân giác của góc.
Lời giải:
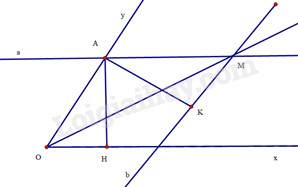
Gọilà giao điểm của đường thẳngvới tia,là giao điểm của đường thẳngvới tia. Kẻvuông góc vớitạivuông góc vớitại. Do khoảng cách giữa hai lề của thước là không đổi nên ta có.
Tứ giáccónênlà hình bình hành. Suy ra. Do đó.
(cạnh góc vuông – góc nhọn kề). Suy ra.
Hình bình hànhcónênlà hình thoi. Vậylà tia phân giác của góc.
Bài 30 trang 100 SBT Toán 8 Tập 1 : Cho hình thoicócm,. Các điểmthay đổi lần lượt trên cạnhsao cho.
a) Chứng minhkhông đổi
b) Xác định vị trí của các điểmđể độ dàingắn nhất. Tính độ dài ngắn nhất đó.
Lời giải:
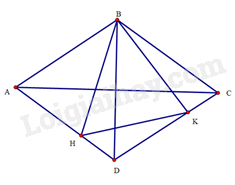
a) Dolà hình thoi nên
Mà, suy ra. Do đó tam giáccân tại. Suy ra.
Mà, suy ra.
(g.c.g). Suy ra. Do đó.
Vậykhông đổi
b) Donên.
Tam giáccóvànên tam giáclà tam giác đều.
Suy ra.
Do đó, độ dàingắn nhất khivàngắn nhất. Vậylần lượt là hình chiếu củatrên.
Khi đó(cạnh huyền – cạnh góc vuông)
Suy ra
Trong tam giácvuông tại, ta có:. Suy ra ta tính được. Vậy độ dài ngắn nhất củalàcm.
=============
THUỘC: GIẢI SÁCH BÀI TẬP MÔN TOÁN LỚP 8 – Cánh diều
