GIẢI CHI TIẾT SÁCH BÀI TẬP toán lớp 8 Bài 5: Hình chữ nhật – Sách Cánh diều
================
Giải SBT Toán 8 Bài 5: Hình chữ nhật
Bài 21 trang 97 SBT Toán 8 Tập 1 : Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?
a) Hình thang có hai cạnh góc vuông là hình chữ nhật
b) Hình thang cân có một góc vuông là hình chữ nhật
c) Hình bình hành có một góc vuông là hình chữ nhật
d) Tứ giác có hai góc vuông là hình chữ nhật.
Lời giải:
a) Sai
b) Đúng
c) Đúng
d) Sai
Bài 22 trang 97 SBT Toán 8 Tập 1 : Hình 20 mô tả mặt phẳng cắt ngang tầng trệt của một ngôi nhà. Biếtvà. Tính độ dài(làm tròn kết quả đến hàng phần mười của mét).
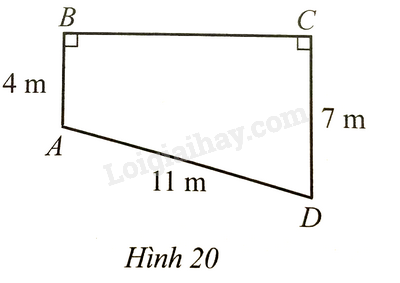
Lời giải:
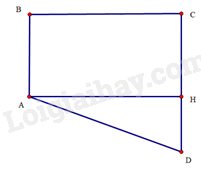
Kẻvuông góc vớitại(Hình 42)
Tứ giáccónênlà hình chữ nhật. Suy ra
Do đó
Trong tam giácvuông tại, ta có:
Suy ra
Do đó
Ta có:(vìlà hình chữ nhật) nên
Bài 23 trang 97 SBT Toán 8 Tập 1 : Cho hình chữ nhậtcó hai đường chéovàcắt nhau tại. Lấy điểmthuộc đoạn thẳng. Gọilần lượt là hình chiếu của điểmtrên đường thẳng. Chứng minh:
a) Tứ giáclà hình chữ nhật.
b) .
Lời giải:
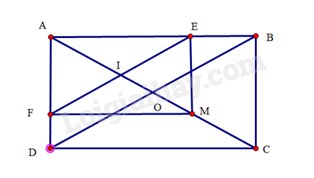
Gọilà giao điểm củavà
a) Tứ giáccónênlà hình chữ nhật.
b) Dovàlà hình chữ nhật nênvànull. Suy ra tam giáccân tạivà tam giáccân tại.
Do đóvàhay.
Màvànằm ở vị trí đòng vị, suy ra.
Bài 24 trang 97 SBT Toán 8 Tập 1 : Cho tam giáccân tạicó các đường trung tuyếncắt nhau tại. Trên tia đối của tialần lượt lấy các điểmsao cho. Tứ giáclà hình gì? Vì sao?
Lời giải:
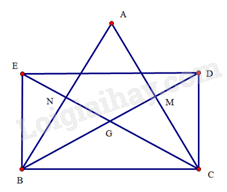
Tứ giáccó hai đường chéovàcắt nhau tại trung điểmcủa mỗi đường nênlà hình bình hành.
Ta có:nên.
(c.g.c). Suy ra.
Dolà trọng tâm của tam giácnên
và
Do đó. Màlà trung điểm củavà, suy ra
Hình bình hànhcónênlà hình chữ nhật.
Bài 25 trang 97 SBT Toán 8 Tập 1 : Cho tam giácvuông cân tại. Lấy điểmthuộc cạnh huyền. Gọilần lượt là hình chiếu của điểmtrên đường thẳng.
a) Tứ giáclà hình gì? Vì sao?
b) Gọilà trung điểm của. Chứng minh ba điểmthẳng hàng
c) Chứng minh khi điểmthay đổi vị trí trên cạnhthì chu vi của tứ giáckhông đổi.
Lời giải:
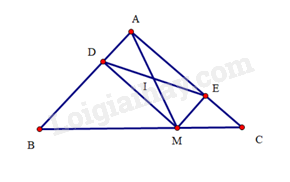
a) Tứ giáccónênlà hình chữ nhật.
b) Dolà hình chữ nhật nên hai đường chéovàcắt nhau tại trung điểm của mỗi đường.
Màlà trung điểm của, suy ralà trung điểm của. Vậy ba điểmthẳng hàng.
c) Dolà hình chữ nhật nên. Suy ra(hai góc so le trong). Mà(vì tam giácvuông cân tại, suy ra. Do đó, tam giáccân tại. Suy ra.
Chu vi hình chữ nhậtlà:
Màkhông đổi nên chu vi của tứ giáckhông đổi.
d)
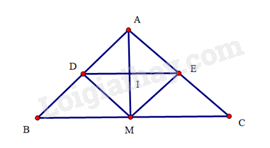
Dolà hình chữ nhật nên
Suy racó độ dài nhỏ nhất khicó độ dài nhỏ nhất. vậylà hình chiếu củatrên đường thẳng.
Trong tam giácvuông cân tạita có
và
Suy ra
(cạnh góc vuông – góc nhọn). Suy ra
Tam giácvuông tạicónên. Suy ra tam giácvuông cân tại. Do đó. Vậy.
=============
THUỘC: GIẢI SÁCH BÀI TẬP MÔN TOÁN LỚP 8 – Cánh diều
