GIẢI CHI TIẾT SÁCH BÀI TẬP toán lớp 8 Bài 4: Hình bình hành – Sách Cánh diều
================
Giải SBT Toán 8 Bài 4: Hình bình hành
Bài 16 trang 94 SBT Toán 8 Tập 1 : Cho tam giáccó. Từ điểmthuộc cạnh, kẻsong song vớivàsong song với(điểmlần lượt thuộc cạnh). Tính chu vi của tứ giác.
Lời giải:
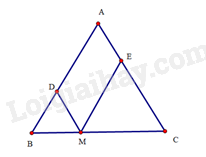
Donên tam giáccân tại. Suy ra.
Mà(hai góc đồng vị), suy ra.
Do đó, tam giáccân tại. Suy ra.
Tứ giáccónênlà hình bình hành. Vậy chu vi của hình bình hànhlà:
Bài 17 trang 94 SBT Toán 8 Tập 1 : Cho tam giáccó các đường trung tuyếnvà. Lấy các điểmsao cholà trung điểm củalà trung điểm của. Chứng minh:
a) Các tứ giáclà hình bình hành;
b)là trung điểm của.
Lời giải:
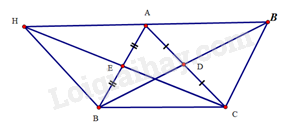
a) Tứ giáccólà trung điểm của hai đường chéovànênlà hình bình hành.
Tương tự, ta chứng minh được tứ giáclà hình bình hành.
b) Dolà hình bình hành nên,. Tương tự,là hình bình hành nên. Suy ra ba điểmthẳng hàng và. Vậylà trung điểm của.
Bài 18 trang 95 SBT Toán 8 Tập 1 : Cho hình bình hành. Trên cạnhlần lượt lấy điểmsao cho. Trên cạnhlần lượt lấy điểmsao cho. Chứng minh:
a) Tứ giáclà hình bình hành;
b) Bốn đường thẳngcùng đi qua một điểm.
Lời giải:
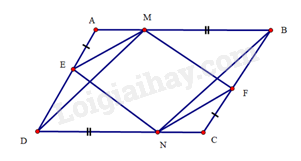
a) Dolà hình bình hành nênvà;và.
Màvà, suy ravà.
(c.g.c). Suy ra
(c.g.c). Suy ra
Tứ giác EFMNcóvànênlà hình bình hành.
b) Tứ giáccóvànênlà hình bình hành.
Dođều là hình bình hành nên các đường chéo của mỗi hình bình hành cắt nhau tại trung điểm của mỗi đường.
Vậycùng đi qua trung điểm của mỗi đường.
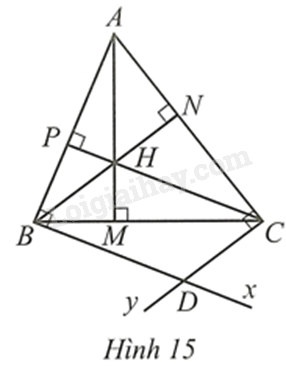
Bài 19 trang 95 SBT Toán 8 Tập 1 : Cho tam giác nhọncó ba đường caocắt nhau tại. Quakẻ tiavuông góc với. Quakẻ tiavuông góc với. Gọilà giao điểm củavà(Hình 15)
a) Chứng minh tứ giáclà hình bình hành;
b) Tam giáccó điều kiện gì thi ba điểmthẳng hàng?
c) Tìm mối liên hệ giữa gócvà góccủa tứ giác.
d) Giả sửlà trung điểm của. Chứng minh diện tích của tam giácbằng diện tích của tứ giác.
Lời giải:
a) Ta có:vànằm ở vị trí đồng vị nên.
Tương tự ta chứng minh được.
Tứ giáccónênlà hình bình hành.
b) Để ba điểmthẳng hàng thìphải thuộc. Màthuộc, suy ralà giao điểm củavà.
Dolà hình bình hành nên hai đường chéovàcắt nhau tại trung điểm của mỗi đường. suy ralà trung điểm.
Khi đó(c.g.c). Suy ra.
Dễ thấy nếu tam giáccóthì ba điểmthẳng hàng.
Vậy tam giáccân tạithìthẳng hàng.
c) Xét tứ giác, ta có:.
Mà, suy ra tính được
Vậy gócvà góccủa tứ giáclà hai góc bù nhau.
d) Dolà trung điểm củanên
Ta có diện tích tam giácbằng:.
Ta chứng minh được(c.c.c.). Suy ra diện tích tứ giácbằng 2 lần diện tích tam giác.
Do đó, diện tích tứ giácbằng:vạy diện tích tam giácbằng điệnt tích của tứ giác.
Bài 20 trang 95 SBT Toán 8 Tập 1 : Cho hình bình hànhcó,. Trên đường thẳng vuông góc vớitạilấy hai điểmsao cho. Trên đường thẳng vuông góc vớitạilấy hai điểmsao cho(Hình 16). Chứng minh:
a) Tứ giáclà hình bình hành;
b) .
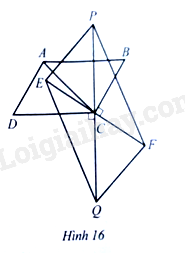
Lời giải:
a) Tứ giáccó hai đường chéovà PQ cắt nhau tại trung điểmcủa mỗi đường nênlà hình binh hành.
b) Gọilà giao điểm củavà,là giao điểm củavà.
Dolà hình bình hành nên,.
Vìnên(hai góc so le trong). Suy ra tam giácvuông tại. Do đó,
Mặt khác, ta cónên.
Xét hai tam giácvà, ta có:
(vì cùng bằng);
Suy ra(c.g.c). Do đó(hai góc tương ứng) hay. Mà, suy ra
Xét tam giác, ta có:
Suy rahay. Vậy.
=============
THUỘC: GIẢI SÁCH BÀI TẬP MÔN TOÁN LỚP 8 – Cánh diều
