Giải SBT Bài 1: Góc và cạnh của một tam giác (C8 SBT Toán 7 Chân trời)

Giải SBT Bài 1: Góc và cạnh của một tam giác (C8 SBT Toán 7 Chân trời)
============\

Giải bài 1 trang 41 SBT Toán 7 Chân trời sáng tạo tập 2 – CTST

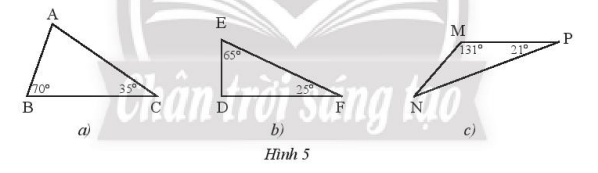
Tìm số đo các góc còn chưa biết của các tam giác ở hình 5

Hướng dẫn giải chi tiết Bài 1

Phương pháp giải

Số đo góc còn lại trong một tam giác bằng \({180^o}\) trừ đi tổng hai góc đã biết.

Lời giải chi tiết

– Xét tam giác ABC ta có:

\(\widehat {{A^{}}} + \widehat B + \widehat C = {180^o}\) suy ra: \(\widehat {{A^{}}} = {180^o} – \widehat B – \widehat C = {180^o} – {70^o} – {35^o} = {75^o}\)

– Xét tam giác EFD ta có:

\(\widehat D + \widehat E + \widehat F = {180^o}\) suy ra: \(\widehat D = {180^o} – \widehat E – \widehat F = {180^o} – {65^o} – {25^o} = {90^o}\)

– Xét tam giác MNP ta có:

\(\widehat M + \widehat N + \widehat P = {180^o}\) suy ra: \(\widehat N = {180^o} – \widehat M – \widehat P = {180^o} – {131^o} – {21^o} = {28^o}\) 

 

–>

— *****

Giải bài 2 trang 41 SBT Toán 7 Chân trời sáng tạo tập 2 – CTST

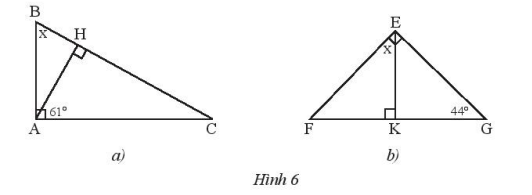
Tìm số đo x trong hình 6

Hướng dẫn giải chi tiết Bài 2

Phương pháp giải

Góc vuông có số đo là \({90^o}\)

Số đo góc còn lại trong một tam giác bằng \({180^o}\) trừ đi tổng hai góc đã biết

Lời giải chi tiết

Hình a:

– Xét tam giác AHC ta có: \(\widehat C = {180^o} – \widehat {{A^{}}} – \widehat H = {180^o} – {61^o} – {90^o} = {29^o}\)

Xét tam giác ABC có: \(\widehat {{A^{}}} + \widehat B + \widehat C = {180^o}\) suy ra: \(x = \widehat B = {180^o} – \widehat A – \widehat C = {180^o} – {90^o} – {29^o} = {61^o}\)

– Xét tam giác EKG có: \(\widehat {GEK} + \widehat {EKG} + \widehat G = {180^o}\)

Suy ra: \(\widehat {GEK} = {180^o} – \widehat {EKG} – \widehat G = {180^o} – {90^o} – {41^o} = {49^o}\)

Mà: \(\widehat {GEK} + \widehat {{\rm{KEF}}} = {90^o}\) suy ra: \(x = \widehat {{\rm{KEF}}} = {90^o} – \widehat {GEK} = {90^o} – {49^o} = {41^o}\)

 

–>

— *****

Giải bài 3 trang 42 SBT Toán 7 Chân trời sáng tạo tập 2 – CTST

Hãy tính tổng 4 góc trong một hình thoi ABCD

Hướng dẫn giải chi tiết Bài 3

Phương pháp giải

Chia hình thoi thành hai hình tam giác.

Lời giải chi tiết

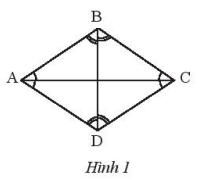
Đường chéo AC chia hình thoi thành hai hình tam giác, ta có tổng 4 góc của một hình thoi ABCD bằng tổng các góc của hai tam giác ABC và ADC và bằng \({360^o}\).

 

–>

— *****

Giải bài 4 trang 42 SBT Toán 7 Chân trời sáng tạo tập 2 – CTST

Trong các bộ ba đoạn thẳng dưới đây, bộ ba nào có thể là độ dài ba cạnh của một tam giác:

a)  1 cm, 7 cm, 9 cm

b) 2 cm, 6 cm, 8 cm

c) 5 cm, 6 cm, 10 cm

Hướng dẫn giải chi tiết Bài 4

Phương pháp giải

Kiểm tra xem bộ ba độ dài có thỏa mãn bất đẳng thức tam giác hay không

Lời giải chi tiết

a) Bộ ba độ dài 1 cm, 7 cm, 9 cm không là độ dài ba cạnh của một tam giác vì không thỏa mãn bất đẳng thức tam giác: 9 > 1 + 7.

b) Bộ ba độ dài 2 cm, 6 cm, 8 cm không là độ dài ba cạnh của một tam giác vì không thỏa mãn bất đẳng thức tam giác: 8 = 2 + 6.

c) Bộ ba độ dài 5 cm, 6 cm, 10 cm có thể là độ dài ba cạnh của một tam giác vì thỏa mãn bất đẳng thức tam giác: 6 – 5 < 10 < 6 + 5

 

–>

— *****

Giải bài 5 trang 42 SBT Toán 7 Chân trời sáng tạo tập 2 – CTST

Cho tam giác ABC có BC = 9 cm, AB = 1 cm. Tìm độ dài cạnh AC, biết độ dài này là một số nguyên.

Hướng dẫn giải chi tiết Bài 5

Phương pháp giải

Sử dụng bất đẳng thức tam giác: BC – AB < AC < BC + AB

Lời giải chi tiết

Ta có: 9 – 1 = 8 < AC < 10 = 9 +1, AC là số nguyên suy ra AC = 9 cm

 

–>

— *****

Giải bài 6 trang 42 SBT Toán 7 Chân trời sáng tạo tập 2 – CTST

Trong một trạm nghiên cứu, người ta đánh dấu ba khu vực M, N, P là ba đỉnh của một tam giác, biết các khoảng cách MN = 30 m, MP – 90 m.

a) Nếu đặt ở khu vực P một trạm phát sóng có bán kính hoạt động 60 m thì tại khu vực N có nhận được tín hiệu không? Vì sao?

b) Cùng câu hỏi như trên với bán kính hoạt động 120 m.

Hướng dẫn giải chi tiết Bài 6

Phương pháp giải

Sử dụng bất đẳng thức tam giác: MP + MN > PN > MP – MN để kiểm tra các điều kiện.

Lời giải chi tiết

a) Áp dụng bất đẳng thức tam giác trong tam giác MNP, ta được:

\(\begin{array}{l}MP + MM > PN > MP – MN\\90 + 30 > PN > 90 – 30\\120 > PN > 60\end{array}\)

Như vậy, với bán kính phát sóng 60 m, khu vực N không thể nhận được tín hiệu.

b) Với bán kính phát sóng 120 m, khu vực N nhận được tín hiệu.

 

–>

— *****