Giải SBT Bài 8: Tính chất ba đường cao của tam giác (C8 SBT Toán 7 Chân trời)

Giải SBT Bài 8: Tính chất ba đường cao của tam giác (C8 SBT Toán 7 Chân trời)
=============

Giải bài 1 trang 63 SBT Toán 7 Chân trời sáng tạo tập 2 – CTST

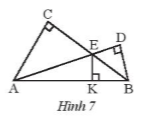
Trong hình 7. Hãy chứng minh AC, EK và BD cùng đi qua một điểm.

Hướng dẫn giải chi tiết Bài 1

Phương pháp giải

Chứng minh M là giao điểm của ba đường cao AC, EK và BD.

Lời giải chi tiết

Gọi M là giao điểm AC và BD.

Xét tam giác MAB có E là giao điểm của hai đường cao AD và BC, do đó E là trực tâm của tam giác MAB.

Suy ra EK phải là đường cao thứ ba ứng với cạnh AB. Dẫn đến EK phải đi qua M.

Vậy AC, EK và BD cùng đi qua điểm M.

–>

— *****

Giải bài 2 trang 63 SBT Toán 7 Chân trời sáng tạo tập 2 – CTST

Cho tam giác ABC cân tại A, vẽ đường trung tuyến AM. Qua A vẽ đường thẳng d vuông góc với AM. Chứng minh d // BC.

Hướng dẫn giải chi tiết Bài 2

Phương pháp giải

Chứng minh d và BC cùng vuông góc với AM.

Lời giải chi tiết

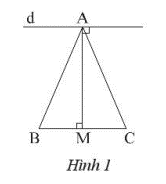
Ta có: \(\Delta AMB = \Delta AMC\) (c – c – c) vì cạnh AM chung, AB = AC (tam giác ABC cân tại A), MB = MC (AM là đường trung tuyến)

Suy ra: \(\widehat {AMB} = \widehat {AMC} = \frac{{{{180}^o}}}{2} = {90^o}\)

Ta có d và BC cùng vuông góc với AM suy ra d // BC.

–>

— *****

Giải bài 3 trang 63 SBT Toán 7 Chân trời sáng tạo tập 2 – CTST

Cho tam giác ABC cân tại A. Vẽ điểm D sao cho A là trung điểm của BD. Vẽ hai đường cao AE và AF của hai tam giác Abc và ACD. Chứng minh góc EAF vuông.

Hướng dẫn giải chi tiết Bài 3

Phương pháp giải

– Sử dụng tính chất của tam giác cân : đường cao cũng là đường phân giác xuất phát từ đỉnh cân.

– Sử dụng: tính chất ba đường cao trong tam giác

Lời giải chi tiết

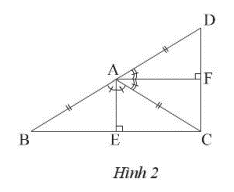
Hai tam giác cân BAC và CAD có hai đường cao AE và BF cũng là đường phân giác của các góc \(\widehat {BAC}\) và \(\widehat {CA{\rm{D}}}\). Do hai góc này kề bù nên AF vuông góc với AE. Suy ra góc EAF vuông.

–>

— *****

Giải bài 4 trang 63 SBT Toán 7 Chân trời sáng tạo tập 2 – CTST

Cho tam giác ABC có \(\widehat {{A^{}}} = {65^o},\widehat B = {54^o}\). Vẽ trực tâm H của tam giác ABC, Tính góc AHB.

Hướng dẫn giải chi tiết Bài 4

Phương pháp giải

– Sử dụng: tính chất ba đường cao trong tam giác.

– Áp dụng: tổng ba góc trong một tam giác bằng \({180^o}\)

Lời giải chi tiết

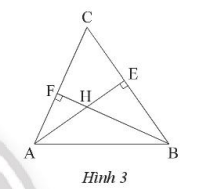
Ta có H là giao điểm của hai đường cao AE và BF.

Trong tam giác vuông ABE ta có:

\(\widehat {E{\rm{A}}B} = {90^o} – \widehat B = {90^o} – {54^o} = {36^o}\)

Trong tam giác vuông BAF ta có:

\(\widehat {FBA} = {90^o} – \widehat {{A^{}}} = {90^o} – {65^o} = {25^o}\)

Trong tam giác AHB ta có:

\(\widehat {AHB} = {90^o} – {36^o} – {25^o} = {119^o}\)

–>

— *****

Giải bài 5 trang 63 SBT Toán 7 Chân trời sáng tạo tập 2 – CTST

Cho tam giác Abc cân tại A có góc A nhọn và H là trực tâm. Cho biết \(\widehat {BHC} = {150^o}\). Tính các góc của tam giác ABC.

Hướng dẫn giải chi tiết Bài 5

Phương pháp giải

Áp dụng: tổng ba góc trong một tam giác bằng \({180^o}\) và đường cao trong tam giác để tính các số đo góc.

Lời giải chi tiết

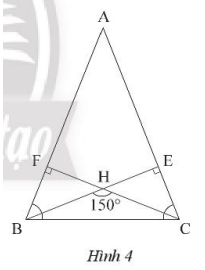
Vẽ hai đường cao BE và CF của tam giác ABC.

Xét tam giác BHC ta có:

\(\widehat {HBC} + \widehat {HCB} = {180^o} – {150^o} = {30^o}\)

Xét hai tam giác vuông BCF và CBE ta có:

\(\widehat B + \widehat C = {180^o} – \left( {\widehat {HBC} + \widehat {HCB}} \right) = {180^o} – {30^o} = {150^o}\)

Do tam giác ABC cân tại A nên ta có:

\(\widehat B = \widehat C = \frac{{{{150}^o}}}{2} = {75^o}\)

\(\widehat {{A^{}}} = {180^o} – {150^o} = {30^o}\)

–>

— *****