Giải SBT Bài 5: Đường trung trực của một đoạn thẳng (C8 SBT Toán 7 Chân trời)

Giải SBT Bài 5: Đường trung trực của một đoạn thẳng (C8 SBT Toán 7 Chân trời)
===========

Giải bài 1 trang 55 SBT Toán 7 Chân trời sáng tạo tập 2 – CTST

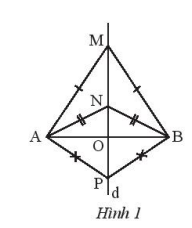
Cho ba tam giác cân MAB, NAB, PAB có chung cạnh đáy AB. Chứng minh ba điểm M, N, P thẳng hàng.

Hướng dẫn giải chi tiết Bài 1

Phương pháp giải

Chứng minh ba điểm M, N, P đều thuộc vào đường trung trưc của AB.

Lời giải chi tiết

Ta có các tam giác cân MAB, NAB, PAB có chung đáy AB, suy ra MA = MB, NA = NB,          

PA = PB. Các điểm M, N, P cùng thuộc đường trung trực của AB nên thẳng hàng.

–>

— *****

Giải bài 2 trang 55 SBT Toán 7 Chân trời sáng tạo tập 2 – CTST

Cho góc xOy bằng \({45^o}\) và điểm M nàm trong góc xOy. Vẽ điểm N sao cho Ox là trung trực của MN, vẽ điểm P sao cho Oy là đường trung trực của MP.

a) Chứng minh ON = OP.

b) Tính số đo góc NOP

Hướng dẫn giải chi tiết Bài 2

Phương pháp giải

Sử dụng tính chất của đường trung trực để chứng minh ON = OP

Lời giải chi tiết

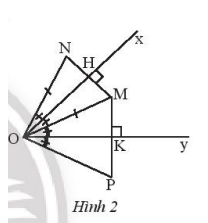
a) Ta có Ox là đường trung trực của MN, suy ra OM = ON

Ta có Oy là đường trung trực của MP, suy ra OM = OP.

Vậy ON = OP.

b) Gọi H và K lần lượt là trung điểm của MN và MP nên HM = HN ; KM = KP

Ta có: \(\Delta OHM = \Delta OHN\) ( vì OH chung, OM = ON, HM = HN)

\(\Delta OKM = \Delta OKP\) (vì OK chung, OM = OP, KM = KP)

Suy ra: \(\widehat {NOP} = \widehat {NOM} + \widehat {MOP} = 2\left( {\widehat {xOM} + \widehat {MOy}} \right) = 2\widehat {xOy} = {2.45^o} = {90^o}\)

–>

— *****

Giải bài 3 trang 55 SBT Toán 7 Chân trời sáng tạo tập 2 – CTST

Cho hai điểm A, B là vị trí của hai nhà máy cùng về mpptj phía bờ sông là đường thẩng a. Vẽ điểm C sao cho a là đường trung trực của AC. Lấy điểm M tùy yá trên a.

a) Chứng minh MA + MB \( \ge \) BC

b) Tìm vị trí của địa điểm \({M_o}\) trên bờ sông để xây dựng một trạm bơm sao cho tổng chiều dài đường ống dẫn nước từ trạm bơm về hai nhà máy là ngắn nhất

Hướng dẫn giải chi tiết Bài 3

Phương pháp giải

Sử dụng với điểm M, B, C tùy ý ta luôn có: MB + MC \( \ge \) BC để suy ra điều chứng minh ở bài toán và tìm vị trí \({M_o}\)

Lời giải chi tiết

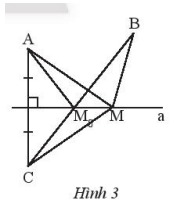
a) Ta có điểm M nàm trên trung trực của AC, suy ra MA = MC.

Với ba điểm tùy ý M, B, C ta luôn có:

\(MB + MC \ge BC\)

Vậy \(MA + MB \ge BC\)

b) Ta có: \(MA + MB \ge BC\), suy ra MA + MB ngắn nhất khi B< C, M thẳng hàng.

Vậy điểm \({M_o}\), cần tìm là giao điểm của đường thẳng BC và đường thẳng a.

–>

— *****