Giải SBT Bài 7: Tính chất ba đường trung tuyến của tam giác (C8 SBT Toán 7 Chân trời)

Giải SBT Bài 7: Tính chất ba đường trung tuyến của tam giác (C8 SBT Toán 7 Chân trời)
===========

Giải bài 1 trang 60 SBT Toán 7 Chân trời sáng tạo tập 2 – CTST

Cho tam giác ABC có trung tuyến AM và G là trọng tâm. Chứng minh:

a) \({S_{AMB}} = {S_{AMC}}\)

b) \({S_{ABG}} = 2{S_{BMG}}\)

c) \({S_{GAB}} = {S_{GBC}} = {S_{GAC}}\) 

Hướng dẫn giải chi tiết Bài 1

Phương pháp giải

So sánh đường cao và các cạnh đáy tương ứng của các tam giác

Lời giải chi tiết

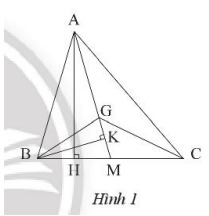
a) Vẽ đường cao AH của tam giác ABC.

Hai tam giác AMB và AMC có cùng đường cao AH và có cạnh đáy bằng nhau: BM = CM

Suy ra: \({S_{AMB}} = {S_{AMC}}\)(vì \({S_{AMB}} = \frac{1}{2}.AH.BM{;^{}}{S_{AMC}} = \frac{1}{2}.AN.CM\))

b) Vẽ đường cao BK của tam giác BGM.

Hai tam giác ABG và BMG có cùng đường cao BK và có cạnh đáy AG = 2MG.

Suy ra: \({S_{ABG}} = \frac{1}{2}.BK.AG = \frac{1}{2}.BK.2MG = 2.\frac{1}{2}.BK.MG = 2{S_{BMG}}\)

c) Ta có:

\({S_{ABG}} = \frac{2}{3}{S_{ABM}} = \frac{1}{3}{S_{ABC}}\)

Tương tự: \({S_{ACG}} = \frac{2}{3}{S_{ACM}} = \frac{1}{3}{S_{ABC}}\)

Suy ra: \({S_{BCG}} = \frac{1}{3}{S_{ABC}}\)

Vậy: \({S_{GAB}} = {S_{GBC}} = {S_{GAC}} = \frac{1}{3}{S_{ABC}}\) 

–>

— *****

Giải bài 2 trang 60 SBT Toán 7 Chân trời sáng tạo tập 2 – CTST

Cho tam giác ABC có đường trung tuyến AM đồng thời là đường phân giác của góc A. Chứng minh tam giác ABC là tam giác cân.

Hướng dẫn giải chi tiết Bài 2

Phương pháp giải

– Chứng minh: \(\Delta AMH = \Delta AMK\)suy ra: MH = MK

– Chứng minh: \(\widehat B = \widehat C\) suy ra tam giác ABC cân

Lời giải chi tiết

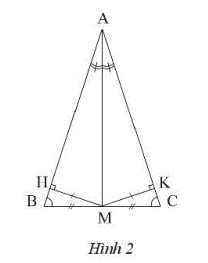
Vẽ đường cao MH của tam giác AMB và vẽ đường cao MK của tam giác AMC.

Ta có \(\Delta AMH = \Delta AMK\)(vì hai tam giác vuông có chung cạnh huyền AM, và một góc nhọn bằng nhau)

Suy ra: MH = MK.

Từ đó, ta có: \(\Delta MBH = \Delta MCK\) (hai tam giác vuông có chung cạnh huyền Am và một cạnh góc vuông bằng nhau: MH = MK)

Suy ra \(\widehat B = \widehat C\)

Vậy tam giác ABC là tam giác cân tại A.

–>

— *****

Giải bài 3 trang 60 SBT Toán 7 Chân trời sáng tạo tập 2 – CTST

Cho tam giác ABC có hai trung tuyến AM và CN cắt nhau tại G.

a) Biết AM = 12 cm, tính AG.

b) Biết GN = 3 cm, tính CN.

c) Tìm x biết AG = 3x – 4, GM = x.

Hướng dẫn giải chi tiết Bài 3

Phương pháp giải

Sử dụng tính chất ba đường trung tuyến của tam giác

Lời giải chi tiết

a) AM = 12 cm, suy ra: \(AG = \frac{2}{3}AM = \frac{2}{3}.12 = 8cm\)

b) GN = 3cm suy ra: CN = 3GN = 3.3= 9cm

c) AG = 2GM, suy ra: 3x – 4 = 2x suy ra x = 4

–>

— *****

Giải bài 4 trang 60 SBT Toán 7 Chân trời sáng tạo tập 2 – CTST

Cho tam giác ABC có ba trung tuyến AM, BN, CP đồng quy tại G. Chứng minh: \(GA + GB + GC = \frac{2}{3}\left( {AM + BN + CP} \right)\)

Hướng dẫn giải chi tiết Bài 4

Phương pháp giải

Sử dụng tính chất của ba đường trung tuyến

Lời giải chi tiết

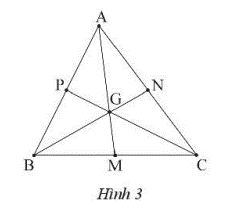
Ta có G là trọng tâm tam giác ANC, do đó ta có:

\(GA = \frac{2}{3}AM;GB = \frac{2}{3}BN;GC = \frac{2}{3}CP\)

Suy ra: \(GA + GB + GC = \frac{2}{3}\left( {AM + BN + CP} \right)\)

–>

— *****

Giải bài 5 trang 60 SBT Toán 7 Chân trời sáng tạo tập 2 – CTST

Cho tam giác ABC có hai đường trung tuyến AM và BN cắt nhau tại G. Vẽ AH vuông góc với BC tại H. Cho biêý HB = HM. Chứng minh:

a) \(\Delta ABH = \Delta AMH\)

b) \(AG = \frac{2}{3}AB\)

Hướng dẫn giải chi tiết Bài 5

Phương pháp giải

– Kiểm tra ba cạnh tương ứng của hai tam giác ABH và tam giác AMH

– Sử dụng tính chất của ba đường trung tuyến

Lời giải chi tiết

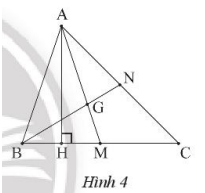
a) Ta có AH là trung trực của đoạn BM, suy ra AB = AM.

Xét hai tam giác ABH và AMH có:

Cạnh AH chung

HB = HM

AB = AM

Suy ra: \(\Delta ABH = \Delta AMH(c – c – c)\)

b) G là trọng tâm tam giác ABC.

Suy ra: \(AG = \frac{2}{3}AM\)

Theo câu a ta có: \(AB = AM\)

Suy ra: \(AG = \frac{2}{3}AB\)

–>

— *****