Giải SBT Bài 2: Tam giác bằng nhau (C8 SBT Toán 7 Chân trời)

Giải SBT Bài 2: Tam giác bằng nhau (C8 SBT Toán 7 Chân trời)
==========

Giải bài 1 trang 45 SBT Toán 7 Chân trời sáng tạo tập 2 – CTST

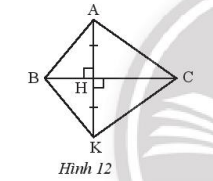
Trong hình 12, tìm tam giác bằng tam giác ABH

Hướng dẫn giải chi tiết Bài 1

Phương pháp giải

Kiểm tra các điều kiện của hai tam giác ABH và KBH.

Lời giải chi tiết

Xét tam giác ABH và tam giác KBH có:

BH chung

\(\widehat {AHB} = \widehat {KHB} = {90^o}\)

AB = KB

Suy ra: \(\Delta ABH = \Delta KBH(c – g – c)\)

 

–>

— *****

Giải bài 2 trang 45 SBT Toán 7 Chân trời sáng tạo tập 2 – CTST

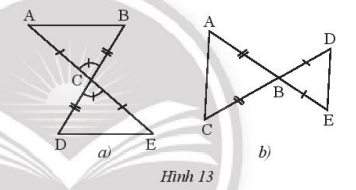
Hai tam giác trong hình 13a, 13b có bằng nhau không? Vì sao?

Hướng dẫn giải chi tiết Bài 2

Phương pháp giải

Kiểm tra các trường hợp bằng nhau của hai tam giác bằng nhau.

Lời giải chi tiết

* Hình 13a: Xét \(\Delta ACB\) và \(\Delta ECB\) có:

AC = EC

\(\widehat {ACB} = \widehat {EC{\rm{D}}}\)

BC = DC

Suy ra: \(\Delta ACB = \Delta EC{\rm{D}}(c – g – c)\)

* Hình 14a: Hai tam giác ABC và DBC không bằng nhau vì hai tam giác ABC và DBC không có hoặc góc tương ứng nào bằng nhau.

 

–>

— *****

Giải bài 3 trang 45 SBT Toán 7 Chân trời sáng tạo tập 2 – CTST

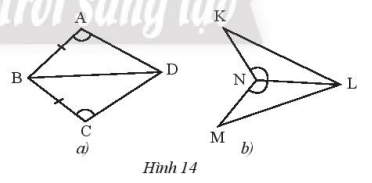
Nêu thêm điều kiện để hai tam giác trong hình 14a, 14b bằng nhau theo trường hợp cạnh – góc – cạnh.’

Hướng dẫn giải chi tiết Bài 3

Phương pháp giải

Xét các điều kiện về hai cạnh và góc xen giữa để đưa ra các điều kiện cho hợp lí

Lời giải chi tiết

* Hình 14a: Xét \(\Delta AB{\rm{D}}\) và \(\Delta CB{\rm{D}}\) có:

AB = BC

\(\widehat {BA{\rm{D}}} = \widehat {BC{\rm{D}}}\)

Để \(\Delta AB{\rm{D}}\) = \(\Delta CB{\rm{D}}\)(c – g – c) thì cần thêm điều kiện AD = CD

* Hình 14b: Xét \(\Delta KNL\) và \(\Delta MNL\) có:

NL chung

\(\widehat {KNL} = \widehat {MNL}\) ( c – g – c) thì cần thêm điều kiện là KN = MN

 

–>

— *****

Giải bài 4 trang 45 SBT Toán 7 Chân trời sáng tạo tập 2 – CTST

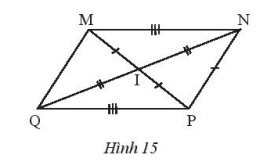
Quan sát hình 15 rồi thay dấu ? bằng tên tam giác thích hợp

a) \(\Delta MNI = \Delta ?\)

b) \(\Delta INM = \Delta ?\)

c) \(\Delta ? = \Delta QIP\)

Hướng dẫn giải chi tiết Bài 4

Phương pháp giải

Xét các điều kiện bằng nhau của hai tam giác

Lời giải chi tiết

a) \(\Delta MNI = \Delta PQI\)( vì có MI = PI, MN = PQ, NI = QI)

b) \(\Delta INM = \Delta IQP\) (vì IN = IQ; NM = QP, IM = IP)

c) \(\Delta NIM = \Delta QIP\) (vì  NI = QI, IM = IP, NM = QP)

 

–>

— *****

Giải bài 5 trang 46 SBT Toán 7 Chân trời sáng tạo tập 2 – CTST

Cho \(\Delta ABC = \Delta D{\rm{EF}}\) và \(\widehat {{A^{}}} = {44^o}\), EF = 7 cm, ED = 15 cm. Tính số đo \(\widehat D\) và độ dài BC, BA.

Hướng dẫn giải chi tiết Bài 5

Phương pháp giải

Từ hai tam giác bằng nhau suy ra các cạnh và các góc tương ứng bằng nhau.

Lời giải chi tiết

Ta có \(\Delta ABC = \Delta D{\rm{EF}}\) suy ra:

\(\widehat D = \widehat {{A^{}}} = {44^o}{,^{}}BC = {\rm{EF = 7(cm)}}{{\rm{,}}^{}}BA = E{\rm{D}} = 15(cm)\)

 

–>

— *****

Giải bài 6 trang 46 SBT Toán 7 Chân trời sáng tạo tập 2 – CTST

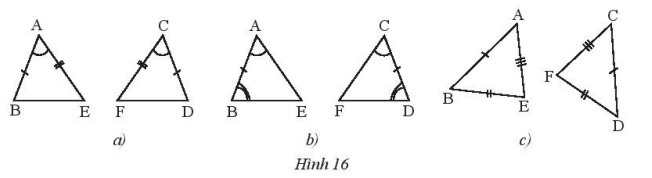
Các cặp tam giác trong Hình 16 có bằng nhau không? Nếu có, chúng bằng nhau theo trường hợp nào?

Hướng dẫn giải chi tiết Bài 6

Phương pháp giải

Kiểm tra các điều kiện theo các trường hợp bằng nhau của hai tam giác

Lời giải chi tiết

a) \(\Delta A{\rm{E}}B = \Delta CF{\rm{D}}\)theo trường hợp canh – góc – cạnh

b) \(\Delta ABE = \Delta C{\rm{D}}F\) theo trường hợp góc – cạnh – góc

c) \(\Delta ABE = \Delta C{\rm{D}}F\)theo trường hợp cạnh – cạnh – cạnh 

 

–>

— *****

Giải bài 7 trang 46 SBT Toán 7 Chân trời sáng tạo tập 2 – CTST

Cho \(\Delta ABC = \Delta D{\rm{EF}}\) và AB = 9 cm, AC = 7 cm, EF = 10 cm. Tính chu vi tam giác ABC.

Hướng dẫn giải chi tiết Bài 7

Phương pháp giải

Từ hai tam giác bằng nhau suy ra các cạnh và các góc tương ứng bằng nhau.

Lời giải chi tiết

Vì \(\Delta ABC = \Delta D{\rm{EF}}\) nên BC = EF = 10 (cm)

Do đó, chu vi tam giác ABC là: 9 + 7 + 10 = 26 (cm)

 

–>

— *****

Giải bài 8 trang 46 SBT Toán 7 Chân trời sáng tạo tập 2 – CTST

Cho tam giác ABC có AB = AC, lấy điểm M trên cạnh BC sao cho BM = CM. Chứng minh hai tam giác ABM và ACM bằng nhau.

Hướng dẫn giải chi tiết Bài 8

Phương pháp giải

Xét các điều kiện về cạnh về góc để xem hai tam giác bằng nhau trong trường hợp nào?

Lời giải chi tiết

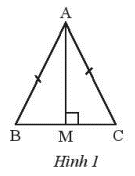
Xét hai tam giác ABM và ACM có:

AB = AC

BM = CM (giả thiết)

AM là cạnh chung

Suy ra: \(\Delta ABM = \Delta ACM(c – c – c)\)

 

–>

— *****

Giải bài 9 trang 46 SBT Toán 7 Chân trời sáng tạo tập 2 – CTST

Cho góc xOy. Lấy hai điểm A, B thuộc tia Ox sao cho OA < OB. Lấy hai điểm C, D thuộc tia Oy sao cho OA = OC, OB = OD. Gọi M là giao điểm của AD và CB. Chứng minh rằng:

a) AD = CB

b) \(\Delta MAB = \Delta MC{\rm{D}}\)

Hướng dẫn giải chi tiết Bài 9

Phương pháp giải

– Chứng minh hai tam giác chưa hai cạnh tương ứng bằng nhau.

– Xét các điều kiện của hai tam giác MAB và MCD xem hai tam đó bằng nhau theo trường hợp nào?

Lời giải chi tiết

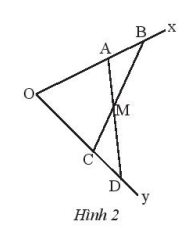
a) Xét tam giác AOD và tam giác COB có:

OA = OC

\(\widehat O\) chung

OB = OD

Suy ra: \(\Delta AO{\rm{D}} = \Delta COB(c – g – c)\)

b) Ta có: \(\Delta AO{\rm{D}} = \Delta COB(c – g – c)\)(chứng minh trên)

Xét tam giác MAB và tam giác MCD có:

Do đó: \(\widehat {MBA} = \widehat {M{\rm{D}}C};\widehat {MAB} = \widehat {MC{\rm{D}}}\) (cùng bù hai góc bằng nhau)

 AB = CD (vì OA = OC, OB = OD)

Suy ra: \(\Delta MAB = \Delta MC{\rm{D(g – c – g)}}\)

 

–>

— *****