Giải SBT Cuối chương 8 – SBT Toán 7 Chân trời

Giải SBT Cuối chương 8 – SBT Toán 7 Chân trời
============

Giải bài 1 trang 65 SBT Toán 7 Chân trời sáng tạo tập 2 – CTST

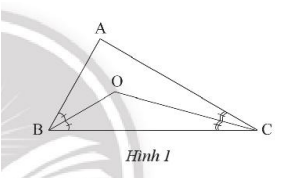
Cho tam giác ABC có \(\widehat {{A^{}}} = \widehat B + \widehat C\). Hai đường phân giác của góc B và góc C cắt nhau tại O.

a) Tính số đo góc A.

b) Tính số đo góc POC.

Hướng dẫn giải chi tiết Bài 1

Phương pháp giải

Tổng ba góc trong một tam giác bằng \({180^o}\) suy ra số đo các góc.

Lời giải chi tiết

a) Ta có: \(\widehat {A{}^{}} = \widehat B + \widehat C = \frac{{{{180}^o}}}{2} = {90^o}\) ( vì \(\widehat {A{}^{}} + \widehat B + \widehat C = {180^o}\))

b) Trong tam giác OBC ta có:

\(\widehat {BOC} = {180^o} – \frac{{\widehat B + \widehat C}}{2} = {180^o} – {45^o} = {135^o}\)

 

–>

— *****

Giải bài 2 trang 65 SBT Toán 7 Chân trời sáng tạo tập 2 – CTST

Cho tam giác ABC có M là điểm đồng quy của ba đường phân giác. Qua M vẽ đường thẳng song song với Bc và cắt AB, AC lần lượt tại N và P. Chứng minh rằng: NP = BN + CP.

Hướng dẫn giải chi tiết Bài 2

Phương pháp giải

– Chứng minh MN = BN

– Chứng minh MP = CP

Suy ra: NP = MN + MP = BN + CP

Lời giải chi tiết

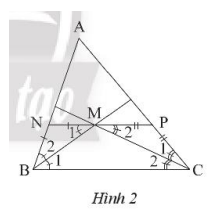
Ta có MN // BC, do đó \(\widehat {{M_1}} = \widehat {{B_1}}\) (so le trong)

Dẫn đến \(\widehat {{M_1}} = \widehat {{B_2}}\)(cùng bằng \(\widehat {{B_1}}\)), suy ra tam giác NMB cân tại N nên  MN = BN

Ta có MP // BC, do đó \(\widehat {{M_2}} = \widehat {{C_2}}\) (so le trong)

Dẫn đến \(\widehat {{M_2}} = \widehat {{C_1}}\)(cùng bằng \(\widehat {{C_2}}\)), suy ra tam giác PMC cân tại P nên  MP = CP

Ta có: NP = MN + MP = BN + CP.

 

–>

— *****

Giải bài 3 trang 65 SBT Toán 7 Chân trời sáng tạo tập 2 – CTST

Cho tam giác ABC có M là giao điểm  của hai đường phân giác của góc B và góc C. Cho biết \(\widehat {BMC} = {132^o}\). Tính số đo các góc \(\widehat {MAB}\) và \(\widehat {MAC}\).

Hướng dẫn giải chi tiết Bài 3

Phương pháp giải

Sử dụng tính chất tia phân giác của các góc trong một tam giác để tính số đo góc cần tìm.

Lời giải chi tiết

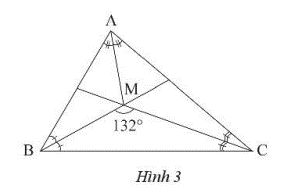
Ta có \(\widehat {MBC} + \widehat {MCB} = {180^o} – \widehat {BMC} = {180^o} – {132^o} = {48^o}\)

Do BM và CM là phân giác các góc \(\widehat B\) và \(\widehat C\) của tam giác ABC nên ta có:

\(\widehat B + \widehat C = 2\left( {\widehat {MBC} + \widehat {MCB}} \right) = {2.48^o} = {96^o}\)

Suy ra: \(\widehat {{A^{}}} = {180^o} – \left( {\widehat B + \widehat C} \right) = {180^o} – {96^o} = {84^o}\)

Do AM là phân giác của góc A của tam giác ABC nên ta có:

\(\widehat {MAB} = \widehat {MAC} = \frac{{\widehat {{A^{}}}}}{2} = \frac{{{{84}^o}}}{2} = {42^o}\)

 

–>

— *****

Giải bài 4 trang 65 SBT Toán 7 Chân trời sáng tạo tập 2 – CTST

Cho tam giác ABC có AB > AC. Trên tia đối của tia BC lấy điểm M sao cho BM  = BA. Trên tia đối của tia CB lấy điểm N sao cho CN = CA.

a) Hãy so sánh các góc \(\widehat {AMB}\) và \(\widehat {ANC}\).

b) Hãy so sánh các đoạn AM và AN.

Hướng dẫn giải chi tiết Bài 4

Phương pháp giải

Sử dụng mỗi quan hệ giữa góc và cạnh đối diện trong một tam giác để so sánh các góc, các cạnh.

Lời giải chi tiết

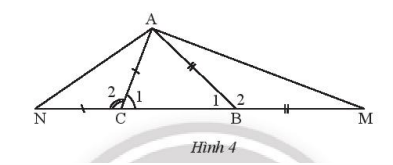
a) Ta có AB > AC do đó \(\widehat {ACB} > \widehat {ABC}\) suy ra \(\widehat {ACN} < \widehat {ABM}\)(1)

Vì tam giác ANC có CN = CA nên tam giác ANC cân tại C suy ra: \(\widehat {ANC} = \widehat {NAC} = \frac{{{{180}^o} – \widehat {ACN}}}{2}\) (2)

Vì tam giác ABM có BM = BA nên tam giác ABM cân tại B suy ra: \(\widehat {AMB} = \widehat {MAB} = \frac{{{{180}^o} – \widehat {ABM}}}{2}\) (3)

 Từ (1), (2) và (3) suy ra \(\widehat {ANC} > \widehat {AMB}\)

b) Trong tam giác ANM, ta có \(\widehat {ANC} > \widehat {AMB}\) suy ra AM > AN

 

–>

— *****

Giải bài 5 trang 65 SBT Toán 7 Chân trời sáng tạo tập 2 – CTST

Cho hai đoạn thẳng AB và CD cắt nhau tại O. Tìm điểm M sao cho \(MA + MB + MC + M{\rm{D}}\) nhỏ nhất.

Hướng dẫn giải chi tiết Bài 5

Phương pháp giải

Sử dụng mối quan hệ giữa ba cạnh trong một tam giác.

Lời giải chi tiết

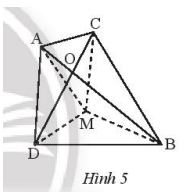
Ta có: \(MA + MB \ge AB,MC + M{\rm{D}} \ge C{\rm{D}}\)

Suy ra: \(MA + MB + MC + M{\rm{D}} \ge AB + C{\rm{D}}\)

MA + MB + MC + MD nhỏ nhất khi và chỉ khi \(MA + MB + MC + M{\rm{D = }}AB + C{\rm{D}}\)

Điều này xảy ra khi M trùng với điểm O.

 

–>

— *****

Giải bài 6 trang 65 SBT Toán 7 Chân trời sáng tạo tập 2 – CTST

a) Chứng minh trong một tam giác, đường cao không lớn hơn đường trung tuyến xuất phát từ cùng một đỉnh.

b) Chứng minh trong một tam giác, đường cao không lớn hơn đường phân giác xuất phát từ cùng một đỉnh.

Hướng dẫn giải chi tiết Bài 6

Phương pháp giải

So sánh đường vuông góc và đường xiên

Lời giải chi tiết

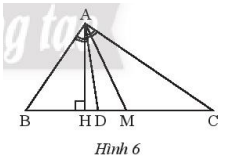
a) Cho tam giác ABC. Vẽ đường cao AH và đường trung tuyến AM, ta có AH là đường vuông góc suy ra \(AH \le AM\)

b) Cho tam giác ABC. Vẽ đường cao AH và đường phân giác AD, ta có AH là đường vuông góc suy ra \(AH \le A{\rm{D}}\)

 

–>

— *****

Giải bài 7 trang 66 SBT Toán 7 Chân trời sáng tạo tập 2 – CTST

Cho tam giác ABC có ba đường phân giác AD, BE, CF đồng quy tại I. Vẽ IH vuông góc với BC tại H. Chứng minh rằng \(\widehat {BIH} = \widehat {CI{\rm{D}}}\).

Hướng dẫn giải chi tiết Bài 7

Phương pháp giải

Sử dụng mối quan hệ giữa các góc trong tam giác để chứng minh

Lời giải chi tiết

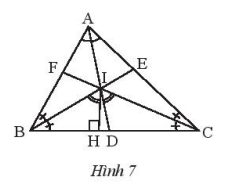
Ta có:

\(\widehat {DIC} = {180^o} – \widehat {AIC} = \widehat {IAC} + \widehat {IC{\rm{A}}} = \frac{{\widehat {{A^{}}} + \widehat C}}{2}\)

Ta có: \(\widehat {BIH} = {90^o} – \frac{{\widehat B}}{2} = \frac{{{{180}^o} – \widehat B}}{2} = \frac{{\widehat {{A^{}}} + \widehat C}}{2} = \widehat {DIC}\)

Suy ra: \(\widehat {BIH} = \widehat {CI{\rm{D}}}\)

 

–>

— *****

Giải bài 8 trang 66 SBT Toán 7 Chân trời sáng tạo tập 2 – CTST

Cho tam giác ABC cân tại A và cho \(\widehat {{A^{}}} = {124^o}\). Vẽ đường cao BH và phân giác BK ứng với đỉnh B của tam giác ABC. Tính số đo các góc của tam giác BHK.

Hướng dẫn giải chi tiết Bài 8

Phương pháp giải

– Tính \(\widehat {HKB} = {42^o}\)

– Xét tam giác vuông BHK, \(\widehat {HBK} = {48^o}\)

Lời giải chi tiết

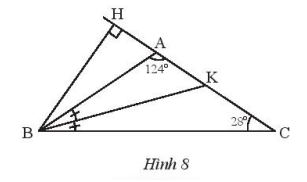
Trong tam giác ABC ta có \(\widehat B = \widehat C = \frac{{{{180}^o} – \widehat {{A^{}}}}}{2} = \frac{{{{180}^o} – {{124}^o}}}{2} = {28^o}\)

Ta có: \(\widehat {HKB} = \widehat {AKB} = {180^o} – {124^o} – {14^o} = {42^o}\)

Trong tam giác vuông BHK ta có: \(\widehat {BHK} = {90^o},\widehat {HBK} = {90^o} – {42^o} = {48^o}\)

 

–>

— *****

Giải bài 9 trang 66 SBT Toán 7 Chân trời sáng tạo tập 2 – CTST

Cho tam giác ABC cân tại A, hai đường cao BE và CF cắt nhau tại H. Chứng minh AH là đường trung trực của BC.

Hướng dẫn giải chi tiết Bài 9

Phương pháp giải

Chứng minh: \(\Delta ABM = \Delta ACM\) suy ra MB = MC.

Lời giải chi tiết

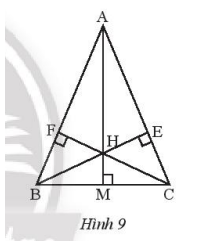
Ta có AH là đường cao vuông góc với cạnh BC tại M.

Xét hai tam giác vuông ABM và ACM có:

Cạnh huyền bằng nhau: AB = AC

Cạnh góc vuông AM chung

Suy ra: \(\Delta ABM = \Delta ACM\) (cạnh huyền – cạnh góc vuông)

Suy ra MB = MC

Vậy AH là đường trung trực của BC

 

–>

— *****

Giải bài 10 trang 66 SBT Toán 7 Chân trời sáng tạo tập 2 – CTST

Cho tam giác nhọn ABC. Hãy nêu cách tìm các điểm sau đây bên trong tam giác ABC.

a) Điểm M cách đều ba đỉnh của tam giác ABC.

b) Điểm N cách đều ba cạnh của tam giác ABC

c) Điểm P là trọng tâm của tam giác ABC.

d) Điểm Q là trực tâm của tam giác ABC.

Hướng dẫn giải chi tiết Bài 10

Phương pháp giải

Sử dụng tính chất ba đường trung trực, phân giác, trung tuyến, đường cao để xác định vị trí các điểm cần tìm.

Lời giải chi tiết

a) Điểm M là giao điểm của hai đường trung trực của tam giác ABC.

b) Điểm N là giao điểm của hai đường phân giác trong của tam giác ABC.

c) Điểm P là giao điểm của hai đường trung tuyến của tam giác ABC.

d) Điểm Q là giao điểm của hai đường cao của tam giác ABC

 

–>

— *****