Sách Toán - Học toán
Giải bài tập Toán từ lớp 1 đến lớp 12, Học toán online và Đề thi toán
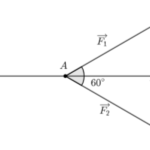
Giải bài 4.12 trang 51 SBT Toán 10 - KN - KẾT NỐI TRI THỨC CỦA BÀI HỌC: Bài 8. Tổng và hiệu của hai vectơ - SBT Toán 10 KNTT ======= Đề bài Trên mặt phẳng, chất điểm \(A\) chịu tác động của ba lực \(\overrightarrow {{F_1}} ,\,\,\overrightarrow {{F_2}} ,\,\,\overrightarrow {{F_3}} \) và ở trạng thái cân bằng. Góc giữa hai … [Đọc thêm...] vềGiải bài 4.12 trang 51 SBT Toán 10 – KN
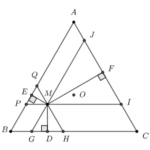
Giải bài 4.18 trang 54 SBT Toán 10 - KN - KẾT NỐI TRI THỨC CỦA BÀI HỌC: Bài 9. Tích của một vectơ với một số - SBT Toán 10 KNTT ======= Đề bài Cho tam giác \(ABC\) đều có trọng tâm \(O.\) \(M\) là một điểm tùy ý nằm trong tam giác. Gọi \(D,\,\,E,\,\,F\) theo thứ tự là hình chiếu vuông góc của \(M\) trên … [Đọc thêm...] vềGiải bài 4.18 trang 54 SBT Toán 10 – KN
Giải bài 4.27 trang 58 SBT Toán 10 - KN - KẾT NỐI TRI THỨC CỦA BÀI HỌC: Bài 10. Vectơ trong mặt phẳng tọa độ - SBT Toán 10 KNTT ======= Đề bài Trong mặt phẳng tọa độ \(Oxy\) cho ba điểm \(A(1;2),\,\,B(3;4)\) và \(C(2; - 1).\) a) Chứng minh rằng \(A,\,\,B,\,\,C\) là ba đỉnh của một tam giác. Tìm tọa độ trọng tâm của tam … [Đọc thêm...] vềGiải bài 4.27 trang 58 SBT Toán 10 – KN
Giải bài 4.34 trang 65 SBT Toán 10 - KN - KẾT NỐI TRI THỨC CỦA BÀI HỌC: Bài 11. Tích vô hướng của hai vectơ - SBT Toán 10 KNTT ======= Đề bài Trong mặt phẳng tọa độ \(Oxy\) cho hai điểm \(A(2;1)\) và \(B(4;3).\) a) Tìm tọa độ của điểm \(C\) thuộc trục hoành sao cho tam giác \(ABC\) vuông tại \(A.\) Tính chu vi và diện … [Đọc thêm...] vềGiải bài 4.34 trang 65 SBT Toán 10 – KN
Giải bài 4.44 trang 67 SBT Toán 10 - KN - KẾT NỐI TRI THỨC CỦA BÀI HỌC: Bài tập cuối chương IV - SBT Toán 10 KNTT ======= Đề bài Cho tam giác \(ABC\) vuông tại \(A\) và \(AB = 3,\,\,AC = 4.\) Độ dài của vectơ \(\overrightarrow {CB} + \overrightarrow {AB} \) bằng A. \(\sqrt {13} \) B. \(2\sqrt {13} \) C. \(4\) D. \(2\) … [Đọc thêm...] vềGiải bài 4.44 trang 67 SBT Toán 10 – KN
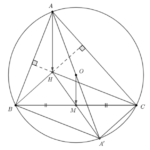
Giải bài 4.5 trang 47 SBT Toán 10 - KN - KẾT NỐI TRI THỨC CỦA BÀI HỌC: Bài 7. Các khái niệm mở đầu - SBT Toán 10 KNTT ======= Đề bài Cho tam giác \(ABC\) không vuông, với trực tâm \(H\), nội tiếp đường tròn \((O).\) Kẻ đường kính \(AA'\) của đường tròn \((O).\) a) Chứng minh rằng \(\overrightarrow {BH} = \overrightarrow … [Đọc thêm...] vềGiải bài 4.5 trang 47 SBT Toán 10 – KN
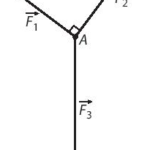
Giải bài 4.11 trang 51 SBT Toán 10 - KN - KẾT NỐI TRI THỨC CỦA BÀI HỌC: Bài 8. Tổng và hiệu của hai vectơ - SBT Toán 10 KNTT ======= Đề bài Trên Hình 4.7 biểu diễn ba lực \(\overrightarrow {{F_1}} ,\,\,\overrightarrow {{F_2}} ,\,\,\overrightarrow {{F_3}} \) cùng tác động vào một vị trí cân bằng \(A.\) Cho biết \(\left| … [Đọc thêm...] vềGiải bài 4.11 trang 51 SBT Toán 10 – KN
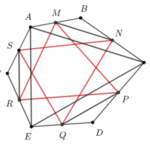
Giải bài 4.17 trang 54 SBT Toán 10 - KN - KẾT NỐI TRI THỨC CỦA BÀI HỌC: Bài 9. Tích của một vectơ với một số - SBT Toán 10 KNTT ======= Đề bài Cho lục giác \(ABCDEF.\) Gọi \(M,\,\,N,\,\,P,\,\,Q,\,\,R,\,\,S\) theo thứ tự là trung điểm của các cạnh \(AB,\;\,BC,\,\,CD,\,\,DE,\,\,EF,\,\,FA.\) Chứng minh rằng hai tam giác … [Đọc thêm...] vềGiải bài 4.17 trang 54 SBT Toán 10 – KN
Giải bài 4.26 trang 58 SBT Toán 10 - KN - KẾT NỐI TRI THỨC CỦA BÀI HỌC: Bài 10. Vectơ trong mặt phẳng tọa độ - SBT Toán 10 KNTT ======= Đề bài Trong mặt phẳng tọa độ \(Oxy\) cho hai điểm \(C(1;6)\) và \(D(11;2).\) a) Tìm tọa độ của điểm \(E\) thuộc trục tung sao cho vectơ \(\overrightarrow {EC} + \overrightarrow … [Đọc thêm...] vềGiải bài 4.26 trang 58 SBT Toán 10 – KN
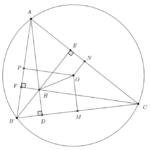
Giải bài 4.33 trang 65 SBT Toán 10 - KN - KẾT NỐI TRI THỨC CỦA BÀI HỌC: Bài 11. Tích vô hướng của hai vectơ - SBT Toán 10 KNTT ======= Đề bài Cho tam giác \(ABC\) không cân. Gọi \(D,\,\,E,\,\,F\) theo thứ tự là chân các đường cao kẻ từ \(A,\,\,B,\,\,C;\) gọi \(M,\,\,N,\,\,P\) tương ứng là trung điểm các cạnh … [Đọc thêm...] vềGiải bài 4.33 trang 65 SBT Toán 10 – KN
