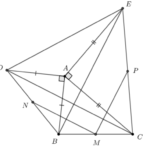
Giải bài 4.31 trang 65 SBT Toán 10 - KN - KẾT NỐI TRI THỨC CỦA BÀI HỌC: Bài 11. Tích vô hướng của hai vectơ - SBT Toán 10 KNTT ======= Đề bài Cho tam giác \(ABC\) có \(\widehat A < {90^ \circ }.\) Dựng ra phía ngoài tam giác hai tam giác vuông cân đỉnh \(A\) là \(ABD\) và \(ACE.\) Gọi \(M,\,\,N,\,\,P\) theo thứ tự là … [Đọc thêm...] vềGiải bài 4.31 trang 65 SBT Toán 10 – KN
Giải sách bài tập toán 10 - Kết nối
Giải bài 4.41 trang 67 SBT Toán 10 – KN
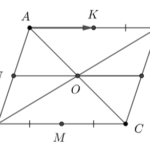
Giải bài 4.41 trang 67 SBT Toán 10 - KN - KẾT NỐI TRI THỨC CỦA BÀI HỌC: Bài tập cuối chương IV - SBT Toán 10 KNTT ======= Đề bài Cho hình bình hành \(ABCD\) tâm \(O\). Gọi \(K,\,\,L,\,\,M,\,\,N\) tướng ứng là trung điểm các cạnh \(AB,\,\,BC,\,\,CD,\,\,DA.\) Trong các vectơ có đầu mút lấy từ các điểm … [Đọc thêm...] vềGiải bài 4.41 trang 67 SBT Toán 10 – KN
Giải bài 4.2 trang 47 SBT Toán 10 – KN
Giải bài 4.2 trang 47 SBT Toán 10 - KN - KẾT NỐI TRI THỨC CỦA BÀI HỌC: Bài 7. Các khái niệm mở đầu - SBT Toán 10 KNTT ======= Đề bài Cho trước hai vectơ không cùng hướng \(\overrightarrow a \) và \(\overrightarrow b \). Hỏi có hay không một vectơ cùng phương với cả \(\overrightarrow a \) và \(\overrightarrow b \)? … [Đọc thêm...] vềGiải bài 4.2 trang 47 SBT Toán 10 – KN
Giải bài 4.8 trang 50 SBT Toán 10 – KN
Giải bài 4.8 trang 50 SBT Toán 10 - KN - KẾT NỐI TRI THỨC CỦA BÀI HỌC: Bài 8. Tổng và hiệu của hai vectơ - SBT Toán 10 KNTT ======= Đề bài Cho hình bình hành \(ABCD\) tâm \(O.\) \(M\) là một điểm tùy ý thuộc cạnh \(BC,\) khác \(B\) và \(C.\) \(MO\) cắt cạnh \(AD\) tại \(N.\) a) Chứng minh rằng \(O\) là trung điểm của … [Đọc thêm...] vềGiải bài 4.8 trang 50 SBT Toán 10 – KN
Bài 4.14 trang 54 SBT Toán 10 – KNTT
Bài 4.14 trang 54 SBT Toán 10 - KNTT - KẾT NỐI TRI THỨC CỦA BÀI HỌC: Bài 9. Tích của một vectơ với một số - SBT Toán 10 KNTT ======= Đề bài Cho tam giác \(OAB\) vuông cân, với \(OA = OB = a.\) Hãy xác định độ dài của các vectơ sau \(\overrightarrow {OA} + \overrightarrow {OB} ,\,\,\overrightarrow {OA} - \overrightarrow {OB} ,\,\,\overrightarrow {OA} + … [Đọc thêm...] vềBài 4.14 trang 54 SBT Toán 10 – KNTT
Giải bài 4.23 trang 58 SBT Toán 10 – KN
Giải bài 4.23 trang 58 SBT Toán 10 - KN - KẾT NỐI TRI THỨC CỦA BÀI HỌC: Bài 10. Vectơ trong mặt phẳng tọa độ - SBT Toán 10 KNTT ======= Đề bài Trong mặt phẳng tọa độ \(Oxy\) cho ba điểm \(A(2; - 1),\,\,B(1;4)\) và \(C(7;0).\) a) Tính độ dài các đoạn thẳng \(AB,\,\,BC\) và \(CA.\) Từ đó suy ra tam giác \(ABC\) là một tam … [Đọc thêm...] vềGiải bài 4.23 trang 58 SBT Toán 10 – KN
Giải bài 4.30 trang 65 SBT Toán 10 – KN
Giải bài 4.30 trang 65 SBT Toán 10 - KN - KẾT NỐI TRI THỨC CỦA BÀI HỌC: Bài 11. Tích vô hướng của hai vectơ - SBT Toán 10 KNTT ======= Đề bài Cho hình chữ nhật \(ABCD\) có \(AB = 1,\,\,BC = \sqrt 2 .\) Gọi \(M\) là trung điểm của \(AD.\) a) Chứng minh rằng các đường thẳng \(AC\) và \(BM\) vuông góc với nhau. b) Gọi \(H\) … [Đọc thêm...] vềGiải bài 4.30 trang 65 SBT Toán 10 – KN
Giải bài 4.40 trang 66 SBT Toán 10 – KN
Giải bài 4.40 trang 66 SBT Toán 10 - KN - KẾT NỐI TRI THỨC CỦA BÀI HỌC: Bài tập cuối chương IV - SBT Toán 10 KNTT ======= Đề bài Cho đoạn thẳng \(AC\) và \(B\) là một điểm nằm giữa \(A,\,\,C.\) Trong các khẳng định sau, khẳng định nào là một khẳng định đúng? A. Hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow … [Đọc thêm...] vềGiải bài 4.40 trang 66 SBT Toán 10 – KN
Giải bài 4.1 trang 47 SBT Toán 10 – KN
Giải bài 4.1 trang 47 SBT Toán 10 - KN - KẾT NỐI TRI THỨC CỦA BÀI HỌC: Bài 7. Các khái niệm mở đầu - SBT Toán 10 KNTT ======= Đề bài Cho tam giác \(ABC\). Gọi \(M\) là trung điểm của cạnh \(BC\) và \(G\) là trọng tâm của tam giác. Trong các khẳng định sau, khẳng định nào là một khẳng định đúng? a) Hai vectơ … [Đọc thêm...] vềGiải bài 4.1 trang 47 SBT Toán 10 – KN
Giải bài 4.7 trang 50 SBT Toán 10 – KN
Giải bài 4.7 trang 50 SBT Toán 10 - KN - KẾT NỐI TRI THỨC CỦA BÀI HỌC: Bài 8. Tổng và hiệu của hai vectơ - SBT Toán 10 KNTT ======= Đề bài Cho hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) không cùng phương. Chứng minh rằng \(\left| {\overrightarrow a } \right| - \left| {\overrightarrow b } \right| < … [Đọc thêm...] vềGiải bài 4.7 trang 50 SBT Toán 10 – KN