Giải bài 4.8 trang 50 SBT Toán 10 – KN

Giải bài 4.8 trang 50 SBT Toán 10 – KN – KẾT NỐI TRI THỨC
CỦA BÀI HỌC: Bài 8. Tổng và hiệu của hai vectơ – SBT Toán 10 KNTT

=======

Đề bài

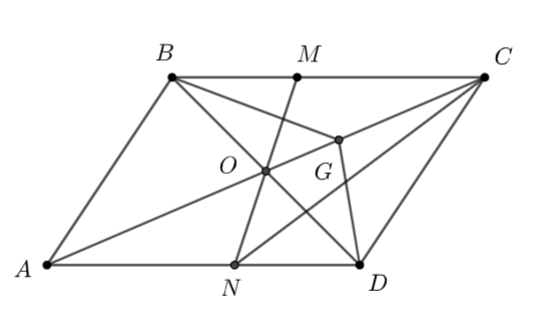
Cho hình bình hành \(ABCD\) tâm \(O.\) \(M\) là một điểm tùy ý thuộc cạnh \(BC,\) khác \(B\) và \(C.\) \(MO\) cắt cạnh \(AD\) tại \(N.\)

a) Chứng minh rằng \(O\) là trung điểm của \(MN.\)

b) Gọi \(G\) là trọng tâm của tam giác \(BCD.\) Chứng minh rằng \(G\) cũng là trọng tâm tam giác \(MNC.\)

Phương pháp giải

–  Chứng minh \(\Delta BOM = \Delta DON\)

–  Chứng minh \(\overrightarrow {BM}  = \overrightarrow {ND} \)

–  Chứng minh \(\overrightarrow {GM}  + \overrightarrow {GN}  + \overrightarrow {GC}  = \overrightarrow 0 \)

Lời giải chi tiết

a)  Xét \(\Delta BOM\) và \(\Delta DON\) có:

\(\widehat {BMO} = \widehat {DNO}\) (2 góc so le trong)

\(OB = OD\)

\(\widehat {BOM} = \overrightarrow {DOC} \) (2 góc đối đỉnh)

\( \Rightarrow \) \(\Delta BOM = \Delta DON\) (g.c.g)

\( \Rightarrow \) \(OM = ON\) (2 cạnh tương ứng)

\( \Rightarrow \) \(O\) là trung điểm của \(MN\)

b)  Ta có: \(G\) là trọng tâm của \(\Delta BCD\)

nên \(\overrightarrow {GB}  + \overrightarrow {GC}  + \overrightarrow {GD}  = \overrightarrow 0 \)

Ta có: \(\Delta BOM = \Delta DON\)

\( \Rightarrow \) \(BM = DN\)

Mặt khác \(BM\)//\(DN\)

\( \Rightarrow \) \(\overrightarrow {BM}  = \overrightarrow {ND} \)

Xét \(\Delta MNC\):

\(\overrightarrow {GM}  + \overrightarrow {GN}  + \overrightarrow {GC}  = \left( {\overrightarrow {GB}  + \overrightarrow {BM} } \right) + \left( {\overrightarrow {GD}  + \overrightarrow {DN} } \right) + \overrightarrow {GC} \)

\( = \left( {\overrightarrow {GB}  + \overrightarrow {GC}  + \overrightarrow {GD} } \right) + \left( {\overrightarrow {BM}  + \overrightarrow {DN} } \right) = \overrightarrow 0 \)

\( \Rightarrow \) \(G\) là trọng tâm của \(\Delta MNC\)

 

============

Thuộc chủ đề:Giải sách bài tập toán 10 – Kết nối