Giải bài 4.10 trang 51 SBT Toán 10 – KN – KẾT NỐI TRI THỨC
CỦA BÀI HỌC: Bài 8. Tổng và hiệu của hai vectơ – SBT Toán 10 KNTT
=======
Đề bài
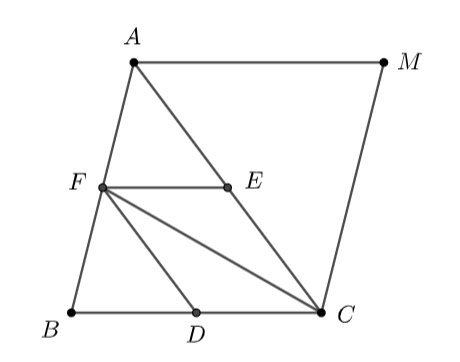
Cho tam giác \(ABC.\) Gọi \(D,\,\,E,\,\,F\) theo thứ tự là trung điểm của các cạnh \(BC,\,\,CA,\,\,AB.\)
a) Xác định vectơ \(\overrightarrow {AF} – \overrightarrow {BD} + \overrightarrow {CE} \)
b) Xác định điểm \(M\) thỏa mãn \(\overrightarrow {AF} – \overrightarrow {BD} + \overrightarrow {CE} = \overrightarrow {MA} .\)
c) Chứng minh rằng \(\overrightarrow {MC} = \overrightarrow {AB} .\)
Phương pháp giải
– Chứng minh \(\overrightarrow {AF} = \overrightarrow {FB} ,\) \(\overrightarrow {BD} = \overrightarrow {DC} \)
– Áp dụng quy tắc hình bình hành với hai vectơ \(\overrightarrow {CE} \) và \(\overrightarrow {CD} \)
– Chứng minh tứ giác \(ABCM\) là hình bình hành
Lời giải chi tiết

a) Ta có: \(DF\) là đường trung bình của \(\Delta ABC\)
\( \Rightarrow \) \(\overrightarrow {CE} = \overrightarrow {DF} \)
\( \Rightarrow \) tứ giác \(CDFE\) là hình bình hành.
Ta có: \(D\) và \(F\) lần lượt là trung điểm của \(BC\) và \(AB\)
\( \Rightarrow \) \(\overrightarrow {AF} = \overrightarrow {FB} ,\) \(\overrightarrow {BD} = \overrightarrow {DC} \)
Ta có: \(\overrightarrow {AF} – \overrightarrow {BD} + \overrightarrow {CE} = \overrightarrow {AF} + \overrightarrow {CD} + \overrightarrow {CE} = \overrightarrow {AF} + \overrightarrow {CF} = \overrightarrow {CF} + \overrightarrow {FB} = \overrightarrow {CB} \)
b) Theo câu a, ta có: \(\overrightarrow {AF} – \overrightarrow {BD} + \overrightarrow {CE} = \overrightarrow {CB} \)
mặt khác \(\overrightarrow {AF} – \overrightarrow {BD} + \overrightarrow {CE} = \overrightarrow {MA} .\)
nên \(\overrightarrow {CB} = \overrightarrow {MA} \)
\( \Rightarrow \) tứ giác \(ABCM\) là hình bình hành
\( \Rightarrow \) \(M\) là điểm đối xứng với \(B\) qua \(E\)
c) Theo câu b, ta có: tứ giác \(ABCM\) là hình bình hành
\( \Rightarrow \) \(\overrightarrow {MC} = \overrightarrow {AB} .\)
============
Thuộc chủ đề:Giải sách bài tập toán 10 – Kết nối
