Giải bất phương trình tích và bất phương trình chứa ẩn ở mấu thức

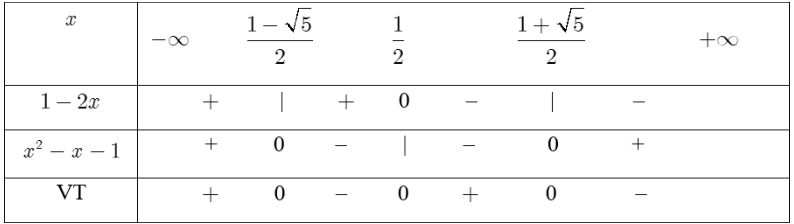
Dạng toán 3. Giải bất phương trình tích và bất phương trình chứa ẩn ở mấu thức.

---

Ví dụ 1 . Giải các bất phương trình:
a) $\left( 1-2x \right)\left( {{x}^{2}}-x-1 \right)>0.$
b) ${{x}^{4}}-5{{x}^{2}}+2x+3\le 0.$

a) Bảng xét dấu:

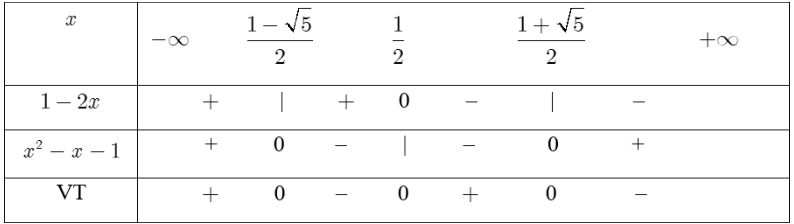
Dựa vào bảng xét dấu, ta có tập nghiệm của bất phương trình đã cho là: ${\rm{S}} = \left( { – \infty ;\frac{{1 – \sqrt 5 }}{2}} \right) \cup \left( {\frac{1}{2};\frac{{1 + \sqrt 5 }}{2}} \right).$
b) Bất phương trình tương đương $({{x}^{4}}-4{{x}^{2}}+4)-({{x}^{2}}-2x+1)\le 0$ $\Leftrightarrow {{({{x}^{2}}-2)}^{2}}-{{(x-1)}^{2}}\le 0$ $\Leftrightarrow ({{x}^{2}}+x-3)({{x}^{2}}-x-1)\le 0.$
Bảng xét dấu:

Dựa vào bảng xét dấu, ta có tập nghiệm của bất phương trình đã cho là: $S=\left[ \frac{-1-\sqrt{13}}{2};\frac{1-\sqrt{5}}{2} \right]\cup \left[ \frac{-1+\sqrt{13}}{2};\frac{1+\sqrt{5}}{2} \right].$

Ví dụ 2 . Giải các bất phương trình:
a) $\frac{{{x}^{2}}-1}{\left( {{x}^{2}}-3 \right)\left( -3{{x}^{2}}+2x+8 \right)}>0.$
b) ${{x}^{2}}+10\le \frac{2{{x}^{2}}+1}{{{x}^{2}}-8}.$

a) Bảng xét dấu:

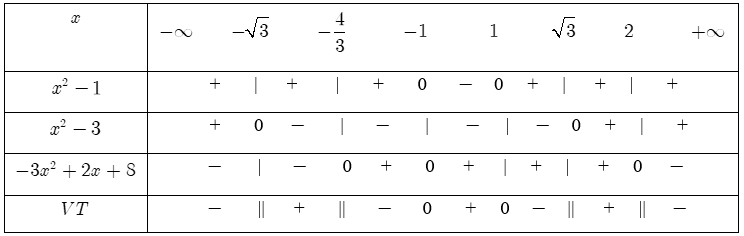
Dựa vào bảng xét dấu, ta có tập nghiệm của bất phương trình đã cho là: $S=\left( -\sqrt{3};-\frac{4}{3} \right)\cup \left( -1;1 \right)\cup \left( \sqrt{3};2 \right).$
b) Ta có: ${x^2} + 10 \le \frac{{2{x^2} + 1}}{{{x^2} – 8}}$ $ \Leftrightarrow \frac{{2{x^2} + 1}}{{{x^2} – 8}} – \left( {{x^2} + 10} \right) \ge 0$ $ \Leftrightarrow \frac{{2{x^2} + 1 – \left( {{x^2} – 8} \right)\left( {{x^2} + 10} \right)}}{{{x^2} – 8}} \ge 0$ $ \Leftrightarrow \frac{{81 – {x^4}}}{{{x^2} – 8}} \ge 0$ $ \Leftrightarrow \frac{{\left( {9 – {x^2}} \right)\left( {9 + {x^2}} \right)}}{{{x^2} – 8}} \ge 0$ $ \Leftrightarrow \frac{{9 – {x^2}}}{{{x^2} – 8}} \ge 0.$
Bảng xét dấu:

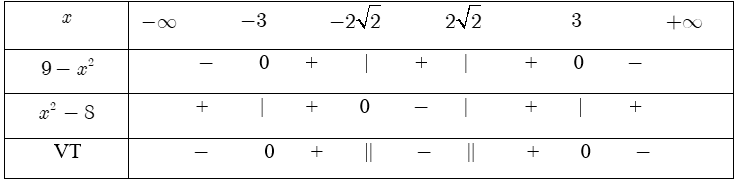
Dựa vào bảng xét dấu, ta có tập nghiệm của bất phương trình đã cho là: $S=[-3;-2\sqrt{2})\cup (2\sqrt{2};3].$

Ví dụ 3 . Giải bất phương trình sau:
a) $\frac{\left| {{x}^{2}}-x \right|-2}{{{x}^{2}}-x-1}\ge 0.$
b) $\frac{\sqrt{{{x}^{2}}+1}-\sqrt{x+1}}{{{x}^{2}}+\sqrt{3}x-6}\le 0.$

a) Vì $\left| {{x}^{2}}-x \right|+2>0$ nên $\frac{\left| {{x}^{2}}-x \right|-2}{{{x}^{2}}-x-1}\ge 0$ $\Leftrightarrow \frac{\left( \left| {{x}^{2}}-x \right|-2 \right)\left( \left| {{x}^{2}}-x \right|+2 \right)}{{{x}^{2}}-x-1}\ge 0$ $\Leftrightarrow \frac{\left( {{x}^{2}}-x-2 \right)\left( {{x}^{2}}-x+2 \right)}{{{x}^{2}}-x-1}\ge 0.$
Bảng xét dấu:

Dựa vào bảng xét dấu, ta có tập nghiệm của bất phương trình đã cho là: $S=(-\infty ;-1]\cup \left( \frac{1-\sqrt{5}}{2};\frac{1+\sqrt{5}}{2} \right)\cup [2;+\infty ).$
b) Điều kiện xác định: $\left\{ \begin{matrix}
x+1\ge 0 \\
{{x}^{2}}+\sqrt{3}x-6\ne 0 \\
\end{matrix} \right.$ $\Leftrightarrow \left\{ \begin{matrix}
x\ge -1 \\
\begin{align}
& x\ne \sqrt{3} \\
& x\ne -2\sqrt{3} \\
\end{align} \\
\end{matrix} \right.$ $\Leftrightarrow \left\{ \begin{matrix}
x\ge -1 \\
x\ne \sqrt{3} \\
\end{matrix} \right.$
Vì $\sqrt {{x^2} + 1} + \sqrt {x + 1} > 0$ nên $\frac{{\sqrt {{x^2} + 1} – \sqrt {x + 1} }}{{{x^2} + \sqrt 3 x – 6}} \le 0$ $ \Leftrightarrow \frac{{\left( {\sqrt {{x^2} + 1} – \sqrt {x + 1} } \right)\left( {\sqrt {{x^2} + 1} + \sqrt {x + 1} } \right)}}{{{x^2} + \sqrt 3 x – 6}} \le 0$ $ \Leftrightarrow \frac{{{x^2} – x}}{{{x^2} + \sqrt 3 x – 6}} \le 0.$
Bảng xét dấu:

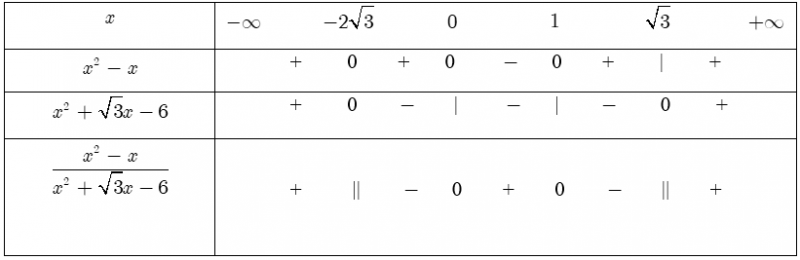
Dựa vào bảng xét dấu và đối chiếu điều kiện, ta có tập nghiệm của bất phương trình đã cho là: $S=\left[ -1;0 \right]\cup [1;\sqrt{3}).$

Ví dụ 4 . Tìm $m$ để bất phương trình $\sqrt{x-{{m}^{2}}-m}\left( 3-\frac{x+1}{{{x}^{3}}-{{x}^{2}}-3x+3} \right)<0$ có nghiệm.

Ta có $\sqrt{x-{{m}^{2}}-m}\left( 3-\frac{x+1}{{{x}^{3}}-{{x}^{2}}-3x+3} \right)<0$ $\Leftrightarrow \left\{ \begin{matrix}
3-\frac{x+1}{{{x}^{3}}-{{x}^{2}}-3x+3}<0 \\
x>{{m}^{2}}+m \\
\end{matrix} \right.$ $\Leftrightarrow \left\{ \begin{matrix}
\frac{\left( x-2 \right)\left( 3{{x}^{2}}+3x-4 \right)}{\left( x-1 \right)\left( {{x}^{2}}-3 \right)}<0 \\
x>{{m}^{2}}+m \\
\end{matrix} \right.$
Bảng xét dấu:

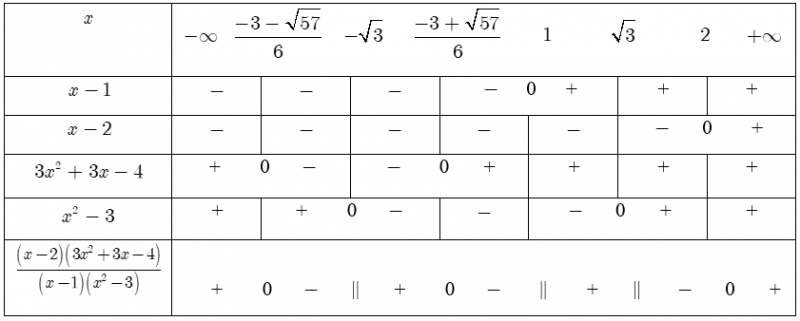
Tập nghiệm của bất phương trình $\frac{\left( x-2 \right)\left( 3{{x}^{2}}+3x-4 \right)}{\left( x-1 \right)\left( {{x}^{2}}-3 \right)}<0$ là: $S=\left( \frac{-3-\sqrt{57}}{6};-\sqrt{3} \right)\cup \left( \frac{-3+\sqrt{57}}{6};1 \right)\cup \left( \sqrt{3};2 \right).$
Do đó bất phương trình đã cho có nghiệm khi và chỉ khi: $\Leftrightarrow {{m}^{2}}+m<2$ $\Leftrightarrow {{m}^{2}}+m-2<0$ $\Leftrightarrow -2<m<1.$
Vậy $-2<m<1$ là giá trị cần tìm.