
Dạng toán 1. Xét dấu của biểu thức chứa tam thức bậc hai.
Phương pháp giải toán : Dựa vào định lí về dấu của tam thức bậc hai để xét dấu của biểu thức chứa tam thức bậc hai.
• Đối với đa thức bậc cao $P(x)$ ta làm như sau:
+ Phân tích đa thức $P\left( x \right)$ thành tích các tam thức bậc hai (hoặc có cả nhị thức bậc nhất).
+ Lập bảng xét dấu của $P\left( x \right).$
• Đối với phân thức $\frac{P(x)}{Q(x)}$ (trong đó $P\left( x \right)$, $Q\left( x \right)$ là các đa thức) ta làm như sau:
+ Phân tích đa thức $P\left( x \right)$, $Q\left( x \right)$ thành tích các tam thức bậc hai (hoặc có cả nhị thức bậc nhất).
+ Lập bảng xét dấu của $\frac{P(x)}{Q(x)}.$
Ví dụ 1 . Xét dấu của các tam thức bậc hai sau:
a) $3{{x}^{2}}-2x+1.$
b) $-{{x}^{2}}+4x+5.$
c) $-4{{x}^{2}}+12x-9.$
d) $3{{x}^{2}}-2x-8.$
e) $25{{x}^{2}}+10x+1.$
f) $-2{{x}^{2}}+6x-5.$
a) Ta có $\Delta’=-2<0$, $a=3>0$ suy ra $3{{x}^{2}}-2x+1>0$, $\forall x\in \mathbb{R}.$
b) Ta có $ – {x^2} + 4x + 5 = 0$ $ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}
{x = – 1}\\
{x = 5}
\end{array}} \right.$
Bảng xét dấu:

Suy ra $-{{x}^{2}}+4x+5>0$ $\Leftrightarrow x\in \left( -1;5 \right)$ và $-{{x}^{2}}+4x+5<0$ $\Leftrightarrow x\in \left( -\infty ;-1 \right)\cup \left( 5;+\infty \right).$
c) Ta có $\Delta’=0$, $a<0$ suy ra $-4{{x}^{2}}+12x-9<0$, $\forall x\in \mathbb{R}\backslash \left\{ \frac{3}{2} \right\}.$
d) Ta có $3{{x}^{2}}-2x-8=0$ $\Leftrightarrow \left[ \begin{matrix}
x=2 \\
x=-\frac{4}{3} \\
\end{matrix} \right.$
Bảng xét dấu:

Suy ra $3{{x}^{2}}-2x-8>0$ $\Leftrightarrow x\in \left( -\infty ;-\frac{4}{3} \right)\cup \left( 2;+\infty \right)$ và $3{{x}^{2}}-2x-8<0$ $\Leftrightarrow x\in \left( -\frac{4}{3};2 \right).$
e) Ta có $\Delta’=0$, $a>0$ suy ra $25{{x}^{2}}+10x+1>0$, $\forall x\in \mathbb{R}\backslash \left\{ -\frac{1}{5} \right\}.$
f) Ta có $\Delta’=-1<0$, $a<0$ suy ra $-2{{x}^{2}}+6x-5<0$, $\forall x\in \mathbb{R}.$
Ví dụ 2 . Tùy theo giá trị của tham số $m$, hãy xét dấu của các biểu thức $f(x)={{x}^{2}}+2mx+3m-2.$
Tam thức $f(x)$ có $a=1>0$ và $\Delta’={{m}^{2}}-3m+2.$
• Nếu $1<m<2$ $\Rightarrow \Delta'<0$ $\Rightarrow f(x)>0$, $\forall x\in R.$
• Nếu $\left[ \begin{align}
& m=1 \\
& m=2 \\
\end{align} \right.$ $\Rightarrow \Delta’=0$ $\Rightarrow f(x)\ge 0$, $\forall x\in R$ và $f(x)=0$ $\Leftrightarrow x=-m.$
• Nếu $\left[ \begin{align}
& m>2 \\
& m<1 \\ \end{align} \right.$ $\Rightarrow \Delta’>0$ $\Rightarrow f(x)$ có hai nghiệm: ${{x}_{1}}=-m-\sqrt{{{m}^{2}}-3m+2}$ và ${{x}_{2}}=-m+\sqrt{{{m}^{2}}-3m+2}$. Khi đó:
+ $f(x)>0$ $\Leftrightarrow x\in (-\infty ;{{x}_{1}})\cup ({{x}_{2}};+\infty ).$
+ $f(x)<0$ $\Leftrightarrow x\in ({{x}_{1}};{{x}_{2}}).$
Ví dụ 3 . Xét dấu của các biểu thức sau:
a) $\left( -{{x}^{2}}+x-1 \right)\left( 6{{x}^{2}}-5x+1 \right).$
b) $\frac{{{x}^{2}}-x-2}{-{{x}^{2}}+3x+4}.$
c) ${{x}^{3}}-5x+2.$
d) $x-\frac{{{x}^{2}}-x+6}{-{{x}^{2}}+3x+4}.$
a) Ta có:
$-{{x}^{2}}+x-1=0$ vô nghiệm.
$6{{x}^{2}}-5x+1=0$ $\Leftrightarrow x=\frac{1}{2}$ hoặc $x=\frac{1}{3}.$
Bảng xét dấu:
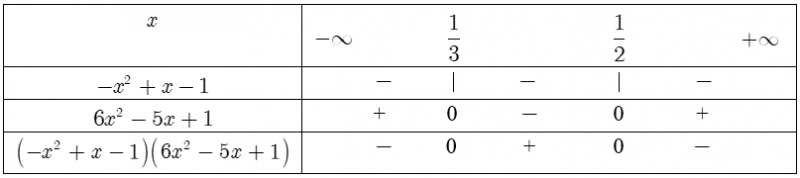
Suy ra $\left( -{{x}^{2}}+x-1 \right)\left( 6{{x}^{2}}-5x+1 \right)$ dương khi và chỉ khi $x\in \left( \frac{1}{3};\frac{1}{2} \right)$, $\left( -{{x}^{2}}+x-1 \right)\left( 6{{x}^{2}}-5x+1 \right)$ âm khi và chỉ khi $x\in \left( -\infty ;\frac{1}{3} \right)\cup \left( \frac{1}{2};+\infty \right).$
b) Ta có:
${{x}^{2}}-x-2=0$ $\Leftrightarrow \left[ \begin{matrix}
x=-1 \\
x=2 \\
\end{matrix} \right.$
$-{{x}^{2}}+3x+4=0$ $\Leftrightarrow \left[ \begin{matrix}
x=-1 \\
x=4 \\
\end{matrix} \right.$
Bảng xét dấu:
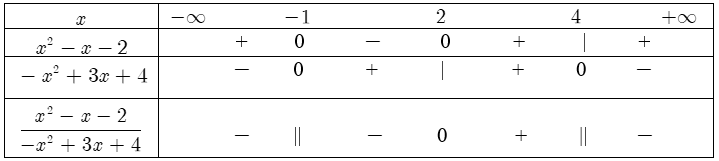
Suy ra $\frac{{{x}^{2}}-x-2}{-{{x}^{2}}+3x+4}$ dương khi và chỉ khi $x\in \left( 2;4 \right)$, $\frac{{{x}^{2}}-x-2}{-{{x}^{2}}+3x+4}$ âm khi và chỉ khi $x\in \left( -\infty ;-1 \right)\cup \left( -1;2 \right)\cup \left( 4;+\infty \right).$
c) Ta có:
${{x}^{3}}-5x+2=\left( x-2 \right)\left( {{x}^{2}}+2x-1 \right).$
${{x}^{2}}+2x-1=0\Leftrightarrow x=-1\pm \sqrt{2}.$
Bảng xét dấu:
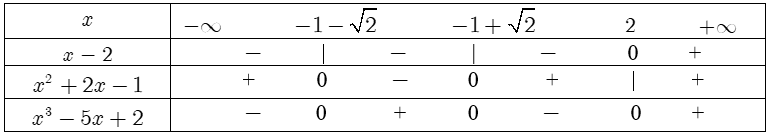
Suy ra ${{x}^{3}}-5x+2$ dương khi và chỉ khi $x\in \left( -1-\sqrt{2};-1+\sqrt{2} \right)\cup \left( 2;+\infty \right)$, ${{x}^{3}}-5x+2$ âm khi và chỉ khi $x\in \left( -\infty ;-1-\sqrt{2} \right)\cup \left( -1+\sqrt{2};2 \right).$
d) Ta có:
$x-\frac{{{x}^{2}}-x+6}{-{{x}^{2}}+3x+4}$ $=\frac{-{{x}^{3}}+2{{x}^{2}}+5x-6}{-{{x}^{2}}+3x+4}$ $=\frac{\left( x-1 \right)\left( -{{x}^{2}}+x+6 \right)}{-{{x}^{2}}+3x+4}.$
$-{{x}^{2}}+x+6=0$ $\Leftrightarrow \left[ \begin{matrix}
x=-2 \\
x=3 \\
\end{matrix} \right.$
$-{{x}^{2}}+3x+4=0$ $\Leftrightarrow \left[ \begin{matrix}
x=-1 \\
x=4 \\
\end{matrix} \right.$
Bảng xét dấu:
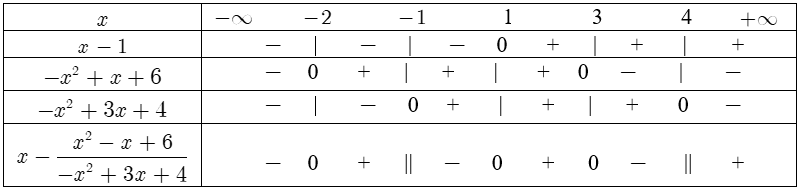
Suy ra $x-\frac{{{x}^{2}}-x+6}{-{{x}^{2}}+3x+4}$ dương khi và chỉ khi $x\in \left( -2;-1 \right)\cup \left( 1;3 \right)\cup \left( 4;+\infty \right)$, $x-\frac{{{x}^{2}}-x+6}{-{{x}^{2}}+3x+4}$ âm khi và chỉ khi $x\in \left( -\infty ;-2 \right)\cup \left( -1;1 \right)\cup \left( 3;4 \right).$
