Lý thuyết bài Dấu của tam thức bậc hai

 LÝ THUYẾT VỀ DẤU CỦA TAM THỨC BẬC HAI

1. Tam thức bậc hai :

• Tam thức bậc hai (đối với $x$) là biểu thức dạng $a{{x}^{2}}+bx+c$, trong đó $a$, $b$, $c$ là những số cho trước với $a\ne 0.$
• Nghiệm của phương trình $a{{x}^{2}}+bx+c=0$ được gọi là nghiệm của tam thức bậc hai $f\left( x \right)=a{{x}^{2}}+bx+c.$
• $\Delta ={{b}^{2}}-4ac$ và $\Delta’=b’^{2}-ac$ theo thứ tự được gọi là biệt thức và biệt thức thu gọn của tam thức bậc hai $f\left( x \right)=a{{x}^{2}}+bx+c.$

2. Dấu của tam thức bậc hai :

ĐỊNH LÍ

Cho \(f(x)=ax^2+bx+c\,(a\neq 0), \Delta = b^2-4ac\)

• Nếu \(\Delta <0\)thì \(f(x)\) luôn cùng dấu với hệ số \(a, \forall x \in \mathbb{R}\)
• Nếu \(\Delta =0\)thì \(f(x)\) luôn cùng dấu với hệ số a trừ khi \(x=-\frac{-b}{2a}\)
• Nếu \(\Delta >0\)thì \(f(x)\) cùng dấu với hệ số a khi \(x<x_1\)hoặc \(x>x_2\), trái dấu với hệ số a khi \(x_1<x<x_2\)

trong đó \(x_1; x_2\,(x_1<x_2)\) là hai nghiệm của \(f(x)\).

CHÚ Ý
Cũng như khi giải phương trình bậc hai, khi xét dấu tam thức bậc hai, ta có thể dùng biểu thức thu gọn $\Delta ‘$thay cho $\Delta $ và cũng được các kết quả tương tự.
Ví dụ 1: $f(x) = 2{x^2} – x + 1 > 0$với mọi $x \in R$ vì tam thức f(x) có$ \Delta  =  – 7 < 0$ và a = 2 > 0

NHẬN XÉT
Từ định lý về dấu của tam thức bậc hai, ta thấy chỉ có một trường hợp duy nhất trong đó dấu của tam thức không thay đổi ( luôn âm hoặc luôn dương), đó là khi $\Delta  < 0$. Lúc đó, dấu của tam thức trùng với dấu của hệ số a. với \(\Delta = b^2-4ac\).

Ta có:

• \(f(x) >0 \quad \forall x \in \mathbb{R} \Leftrightarrow \begin{cases}\Delta <0 \\ a>0\end{cases}\)
• \(f(x) <0 \quad \forall x \in \mathbb{R} \Leftrightarrow \begin{cases} \Delta <0 \\ a<0 \end{cases}\)
• \(f(x) \ge 0 \quad \forall x \in \mathbb{R} \Leftrightarrow \begin{cases} \Delta \le 0 \\ a>0 \end{cases}\)
• \(f(x) \le 0 \quad \forall x \in \mathbb{R} \Leftrightarrow \begin{cases} \Delta \le 0 \\ a<0 \end{cases}\)

Dấu của tam thức bậc hai được thể hiện trong các bảng sau:
• Trường hợp 1: $Δ<0$ (tam thức bậc hai vô nghiệm).

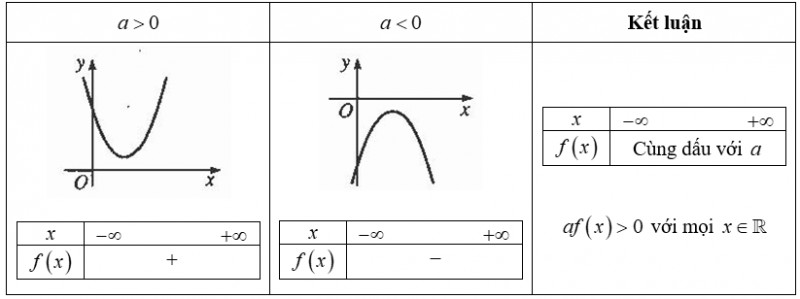
• Trường hợp 2: $Δ=0$ (tam thức bậc hai có nghiệm kép ${x_0} = – \frac{b}{{2a}}$).

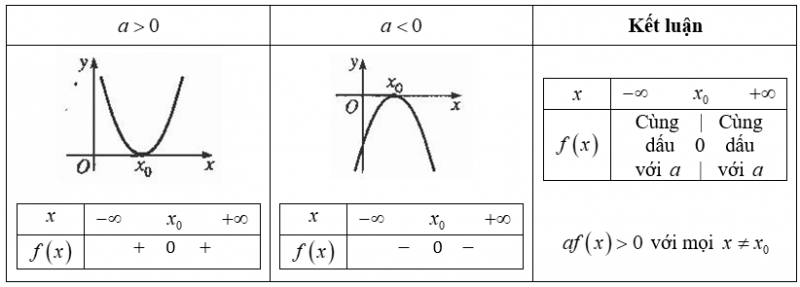
• Trường hợp 3: $Δ>0$ (tam thức bậc hai có hai nghiệm ${x_1}$ và ${x_2}$ $\left( {{x_1} < {x_2}} \right)$).

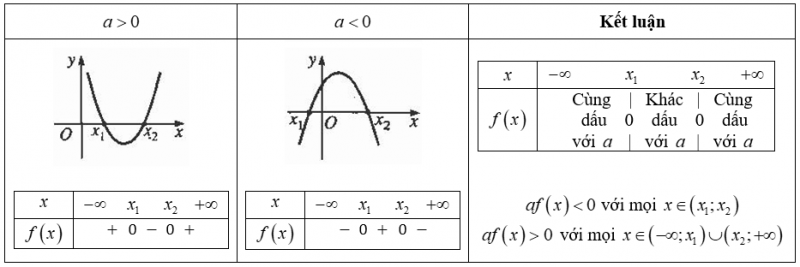
II. Bất phương trình bậc hai một ẩn

1. Bất phương trình bậc hai

Bất phương trình bậc nhất hai ẩn x  là bất phương trình dạng $ax^2+bx+c<0$ (hoặc $ax^2+bx+c>0; ax^2+bx+c \geq 0; ax^2+bx+c \leq 0$

trong đó a, b, c là những số thực đã cho, \(a \neq 0\)

2. Giải bất phương trình bậc hai

Giải bất phương trình bậc hai $ax^2+bx+c<0$thực chất là tìm các khoảng mà trong đó \(f(x)=ax^2+bx+c\) cùng dấu với hệ số a (trường hợp a < 0) hay trái dấu với hệ số a (trường hợp a > 0).