Đề: Biết rằng các đường tiệm cận ngang và tiệm cận đứng của đường cong \(\left( C \right):y = \frac{{5x – 1 – \sqrt {{x^2} – 1} }}{{x – 4}}\) và trục tung cắt nhau tạo thành một đa giác (H). Mệnh đề nào dưới đây đúng?

Xét hàm số \(y = \frac{{5x – 1 – \sqrt {{x^2} – 1} }}{{x – 4}}\)

TXĐ: \(D = \left( { – \infty ; – 1} \right];\left[ {1; + \infty } \right)/\left\{ 4 \right\}\)

Ta có: \(\mathop {\lim y}\limits_{x \to {4^ + }}  = \mathop {\lim }\limits_{x \to {4^ + }} \frac{{5x – 1 – \sqrt {{x^2} – 1} }}{{x – 4}} =  + \infty ;\,\,\mathop {\lim y}\limits_{x \to {4^ – }}  = \mathop {\lim }\limits_{x \to {4^ – }} \frac{{5x – 1 – \sqrt {{x^2} – 1} }}{{x – 4}} =  – \infty \)

\(\mathop {\lim y}\limits_{x \to  – \infty }  = \mathop {\lim }\limits_{x \to  – \infty } \frac{{5x – 1 – \sqrt {{x^2} – 1} }}{{x – 4}} = \mathop {\lim }\limits_{x \to  – \infty } \frac{{5 – \frac{1}{x} + \sqrt {1 – \frac{1}{x}} }}{{1 – \frac{4}{x}}} = 6\)

\(\mathop {\lim y}\limits_{x \to  – \infty }  = \mathop {\lim }\limits_{x \to  – \infty } \frac{{5x – 1 – \sqrt {{x^2} – 1} }}{{x – 4}} = \mathop {\lim }\limits_{x \to  – \infty } \frac{{5 – \frac{1}{x} – \sqrt {1 – \frac{1}{x}} }}{{1 – \frac{4}{x}}} = 4\)

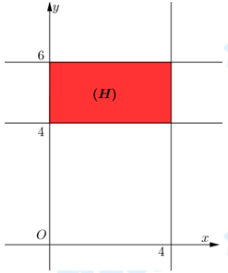
Vậy đồ thị hàm số có các đường tiệm cận đứng và tiệm cận ngang lần lượt là \(x = 4,y = 4,y = 6\) như hình vẽ bên. Khi đó (H) là vùng được tô màu, là một hình chữ nhật có chu vi bằng 12.