Có hai cây cột, một cây cao $12 \text{m}$ và một cây cao $28 \text{m}$ đứng cách nhau $30 \text{m}\text{

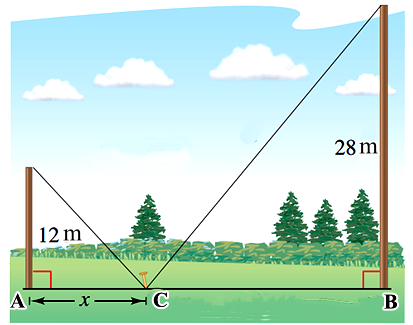
Có hai cây cột, một cây cao $12 \text{m}$ và một cây cao $28 \text{m}$ đứng cách nhau $30 \text{m}\text{.}$ Chúng được giữ bằng hai sợi dây, gắn vào một cọc duy nhất nối từ mặt đất đến đỉnh mỗi cột. Gọi $x$ là khoảng cách từ cột cao $12 \text{m}$ đến cọc.

a) Để tổng chiều dài của dây ngắn nhất thì $x$ có thể là $0$ hoặc $30$.

b) Chiều dài sợi dây nối từ cọc đến đỉnh cột cao $28 \text{m}$ là $\sqrt{1684+{{x}^{2}}}$.

c) Tổng chiều dài của dây là $\sqrt{144+{{x}^{2}}}+\sqrt{1684-60x+{{x}^{2}}}$.

d) Tổng chiều dài ngắn nhất của dây là $50 \text{m}$.

Lời giải: Rõ ràng để tổng chiều dài dây ngắn nhất thì cọc phải nằm trong khoảng giữa hai cây cột nên $x\in \left( 0;30 \right)$.
$AC=x\Rightarrow BC=30-x$.
Chiều dài sợi dây nối từ cọc đến đỉnh cột cao $12 \text{m}$ là $\sqrt{{{12}^{2}}+{{x}^{2}}}=\sqrt{144+{{x}^{2}}}$.
Chiều dài sợi dây nối từ cọc đến đỉnh cột cao $28 \text{m}$ là $\sqrt{{{28}^{2}}+{{\left( 30-x \right)}^{2}}}=\sqrt{1684-60x+{{x}^{2}}}$.
Suy ra tổng chiều dài của sợi dây là $f\left( x \right)=\sqrt{144+{{x}^{2}}}+\sqrt{1684-60x+{{x}^{2}}}$.
Xét hàm số $f\left( x \right)=\sqrt{144+{{x}^{2}}}+\sqrt{1684-60x+{{x}^{2}}}$ với $x\in \left[ 0;30 \right]$.
Ta có ${f}’\left( x \right)=\dfrac{x}{\sqrt{144+{{x}^{2}}}}+\dfrac{x-30}{\sqrt{1684-60x+{{x}^{2}}}}$.
${f}’\left( x \right)=0\Leftrightarrow x\sqrt{1684-60x+{{x}^{2}}}=\left( 30-x \right)\sqrt{144+{{x}^{2}}}$.
Bình phương hai vế ta được:
${{x}^{2}}\left( 1684-60x+{{x}^{2}} \right)={{\left( 30-x \right)}^{2}}\left( 144+{{x}^{2}} \right)$
$\Leftrightarrow 1684{{x}^{2}}-60{{x}^{3}}+{{x}^{4}}=\left( 900-60x+{{x}^{2}} \right)\left( 144+{{x}^{2}} \right)$
$\Leftrightarrow 1684{{x}^{2}}-60{{x}^{3}}+{{x}^{4}}=129600+900{{x}^{2}}-8640x-60{{x}^{3}}+144{{x}^{2}}+{{x}^{4}}$
$\Leftrightarrow 1684{{x}^{2}}=129600+1044{{x}^{2}}-8640x$
$\Leftrightarrow 640{{x}^{2}}+8640x-129600=0$.
Chia cả hai vế cho $160$:
$4{{x}^{2}}+54x-810=0$.
Giải phương trình bậc hai ta được: $x=9$ hoặc $x=-\dfrac{45}{2}$.
Do $x\in \left[ 0;30 \right]$ nên ta nhận $x=9$.
Ta có $f\left( 0 \right)=\sqrt{144}+\sqrt{1684}=12+\sqrt{1684}\approx 12+41,036 = 53,036$.
$f\left( 9 \right)=\sqrt{144+{{9}^{2}}}+\sqrt{1684-60\cdot 9+{{9}^{2}}}=\sqrt{144+81}+\sqrt{1684-540+81}=\sqrt{225}+\sqrt{1225}=15+35=50$.
$f\left( 30 \right)=\sqrt{144+{{30}^{2}}}+\sqrt{1684-60\cdot 30+{{30}^{2}}}=\sqrt{144+900}+\sqrt{1684-1800+900}=\sqrt{1044}+\sqrt{784}\approx 32,31+28=60,31$.
So sánh các giá trị, ta thấy chiều dài ngắn nhất của dây là $50 \text{m}$.
(Sai) Để tổng chiều dài của dây ngắn nhất thì $x$ có thể là $0$ hoặc $30$.
(Vì): Để tổng chiều dài dây ngắn nhất thì cọc phải nằm trong khoảng giữa hai cây cột nên $x\in \left( 0;30 \right)$, không bao gồm các điểm mút.
(Sai) Chiều dài sợi dây nối từ cọc đến đỉnh cột cao $28 \text{m}$ là $\sqrt{1684+{{x}^{2}}}$.
(Vì): $AC=x\Rightarrow BC=30-x$ nên chiều dài sợi dây nối từ cọc đến đỉnh cột cao $28 \text{m}$ là $\sqrt{{{28}^{2}}+{{\left( 30-x \right)}^{2}}}=\sqrt{1684-60x+{{x}^{2}}}$.
(Đúng) Tổng chiều dài của dây là $\sqrt{144+{{x}^{2}}}+\sqrt{1684-60x+{{x}^{2}}}$.
(Vì): Chiều dài sợi dây nối từ cọc đến đỉnh cột cao $12 \text{m}$ là $\sqrt{{{12}^{2}}+{{x}^{2}}}=\sqrt{144+{{x}^{2}}}$. Chiều dài sợi dây nối từ cọc đến đỉnh cột cao $28 \text{m}$ là $\sqrt{{{28}^{2}}+{{\left( 30-x \right)}^{2}}}=\sqrt{1684-60x+{{x}^{2}}}$. Tổng chiều dài của sợi dây là $\sqrt{144+{{x}^{2}}}+\sqrt{1684-60x+{{x}^{2}}}$.
(Đúng) Tổng chiều dài ngắn nhất của dây là $50 \text{m}$.
(Vì): Ta có $f\left( 0 \right)\approx 53,04$; $f\left( 9 \right)=50$; $f\left( 30 \right)=60,31$. Vậy chiều dài ngắn nhất của dây là $50 \text{m}$.