Một cái cổng hình Parabol như hình vẽ sau. Chiều cao \(GH = 4m\), chiều rộng \(AB = 4m\), \(AC = BD = 0,9m\). Chủ nhà làm hai cánh cổng khi đóng lại là hình chữ nhật \(CDEF\) tô đậm có giá là \(1200000\) đồng\(/{m^2}\), còn các phần để trắng làm xiên hoa có giá là \(900000\) đồng\(/{m^2}\). Hỏi tổng số tiền để làm hai phần nói trên gần nhất với số tiền nào dưới đây? A. … [Đọc thêm...] vềMột cái cổng hình Parabol như hình vẽ sau. Chiều cao \(GH = 4m\), chiều rộng \(AB = 4m\), \(AC = BD = 0,9m\). Chủ nhà làm hai cánh cổng khi đóng lại là hình chữ nhật \(CDEF\) tô đậm có giá là \(1200000\) đồng\(/{m^2}\), còn các phần để trắng làm xiên hoa có giá là \(900000\) đồng\(/{m^2}\). Hỏi tổng số tiền để làm hai phần nói trên gần nhất với số tiền nào dưới đây?

Cho hàm số \(f\left( x \right)\) có đạo hàm cấp hai liên tục trên \(\mathbb{R}\) và thoả mãn \(f\left( 0 \right) = f'\left( 0 \right) = 0,\,f''\left( x \right) - \left( {2x + 1} \right){e^x} = f\left( x \right)\) với mọi \(x \in \mathbb{R}\). Giá trị của \(f\left( 2 \right)\) bằng A. \({e^2}\). B. \(2{e^4}\). C. \(2{e^2}\). D. \({e^4}\). Lời giải Ta có: … [Đọc thêm...] vềCho hàm số \(f\left( x \right)\) có đạo hàm cấp hai liên tục trên \(\mathbb{R}\) và thoả mãn \(f\left( 0 \right) = f’\left( 0 \right) = 0,\,f”\left( x \right) – \left( {2x + 1} \right){e^x} = f\left( x \right)\) với mọi \(x \in \mathbb{R}\). Giá trị của \(f\left( 2 \right)\) bằng

  Cho hàm số \(f(x)\) thỏa mãn:\(3f( - x) - 2f(x) = {\tan ^2}x\). Tính thể tích vật thể tròn xoay khi quay quanh \(Ox\) bởi hình phẳng giới hạn bởi đồ thị hàm số \(y = f(x)\), trục \(Ox\), trục tung và đường thẳng \(x = \frac{\pi }{4}\). A. \(\frac{{{\pi ^2}}}{{12}}\). B. \(\frac{\pi }{{12}}\). C. \(\frac{\pi }{2}\). D. \(\frac{{{\pi ^2}}}{2}\). Lời … [Đọc thêm...] về  Cho hàm số \(f(x)\) thỏa mãn:\(3f( – x) – 2f(x) = {\tan ^2}x\). Tính thể tích vật thể tròn xoay khi quay quanh \(Ox\) bởi hình phẳng giới hạn bởi đồ thị hàm số \(y = f(x)\), trục \(Ox\), trục tung và đường thẳng \(x = \frac{\pi }{4}\).

Cho hàm số \(f\left( x \right)\) liên tục không âm trên \(\left[ {0\,;\frac{\pi }{2}} \right]\), thỏa mãn \(f\left( x \right).f'\left( x \right) = \cos x.\sqrt {1 + {f^2}\left( x \right)} \) với mọi \(x \in \left[ {0\,;\frac{\pi }{2}} \right]\) và \(f\left( 0 \right) = 2\sqrt 2 \). Giá trị của \(f\left( {\frac{\pi }{2}} \right)\) bằng A. \(2\). B. \(2\sqrt 2 \). C. … [Đọc thêm...] vềCho hàm số \(f\left( x \right)\) liên tục không âm trên \(\left[ {0\,;\frac{\pi }{2}} \right]\), thỏa mãn \(f\left( x \right).f’\left( x \right) = \cos x.\sqrt {1 + {f^2}\left( x \right)} \) với mọi \(x \in \left[ {0\,;\frac{\pi }{2}} \right]\) và \(f\left( 0 \right) = 2\sqrt 2 \). Giá trị của \(f\left( {\frac{\pi }{2}} \right)\) bằng

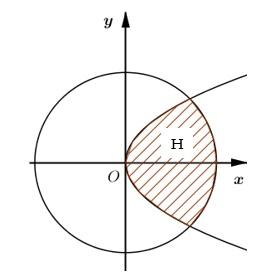
  Cho hình \(H\) giới hạn bởi các đường \({y^2} = 2x\) và \({x^2} + {y^2} = 8\)( phần gạch sọc trong hình). Khối tròn xoay khi quay \(H\) xung quanh trục \(Ox\) có thể tích bằng bao nhiêu? A. \(\frac{{2\pi \left( {8\sqrt 2  - 7} \right)}}{3}\). B. \(\frac{{4\pi \left( {13 - 8\sqrt 2 } \right)}}{3}\). C. \(\left( {\frac{{32\sqrt 2 }}{3} - 8} \right)\pi … [Đọc thêm...] về  Cho hình \(H\) giới hạn bởi các đường \({y^2} = 2x\) và \({x^2} + {y^2} = 8\)( phần gạch sọc trong hình). Khối tròn xoay khi quay \(H\) xung quanh trục \(Ox\) có thể tích bằng bao nhiêu?

Cho \(f\left( x \right)\) là hàm liên tục trên \(\mathbb{R}\). Với số thực \(a > 0\), giả sử rằng mọi \(x \in \left[ {0;a} \right]\) ta có \(f\left( x \right) > 0\) và \(f\left( x \right)f\left( {a - x} \right) = 1\). Tính \(I = \int\limits_0^a {\frac{1}{{1 + f\left( x \right)}}{\rm{d}}x} \). A. \(\frac{a}{3}\). B. \(2a\). C. \(a\ln \left( {1 + a} … [Đọc thêm...] vềCho \(f\left( x \right)\) là hàm liên tục trên \(\mathbb{R}\). Với số thực \(a > 0\), giả sử rằng mọi \(x \in \left[ {0;a} \right]\) ta có \(f\left( x \right) > 0\) và \(f\left( x \right)f\left( {a – x} \right) = 1\). Tính \(I = \int\limits_0^a {\frac{1}{{1 + f\left( x \right)}}{\rm{d}}x} \).

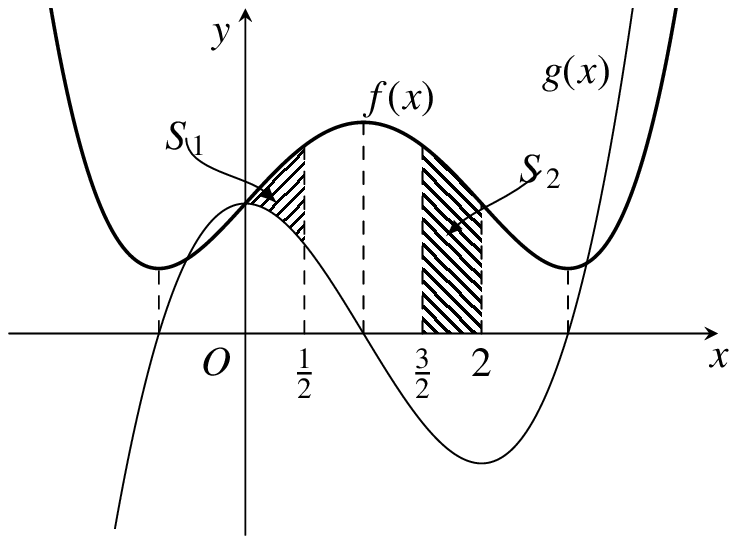
Cho hàm số \(f(x) = a{x^4} - {x^3} + 2x + 2\) và hàm số \(g(x) = b{x^3} + c{x^2} + 2\), có đồ thị như hình vẽ bên. Gọi \({S_1};{S_2}\) là diện tích các hình phẳng gạch chéo trong hình vẽ, biết \({S_2} = \frac{{791}}{{640}}\). Khi đó \({S_1}\) bằng A. \(\frac{{231}}{{640}}\). B. \(\frac{{271}}{{320}}\). C. \(\frac{{571}}{{640}}\). D. … [Đọc thêm...] vềCho hàm số \(f(x) = a{x^4} – {x^3} + 2x + 2\) và hàm số \(g(x) = b{x^3} + c{x^2} + 2\), có đồ thị như hình vẽ bên. Gọi \({S_1};{S_2}\) là diện tích các hình phẳng gạch chéo trong hình vẽ, biết \({S_2} = \frac{{791}}{{640}}\). Khi đó \({S_1}\) bằng

Cho hàm số \(f\left( x \right)\) liên tục và luôn nhận giá trị dương trên khoảng \(\left( {2;4} \right)\), thỏa mãn \(f\left( 3 \right) = \frac{1}{{{e^2}}}\) và \({f^3}\left( x \right) + {e^{ - 2x}} = 3{e^{ - x}}\sqrt {f\left( x \right)} .f'\left( x \right),\;\;\forall x \in \left( {2;4} \right)\). Khi đó \(f\left( {\frac{5}{2}} \right)\) thuộc khoảng A. \(\left( {1;2} … [Đọc thêm...] vềCho hàm số \(f\left( x \right)\) liên tục và luôn nhận giá trị dương trên khoảng \(\left( {2;4} \right)\), thỏa mãn \(f\left( 3 \right) = \frac{1}{{{e^2}}}\) và \({f^3}\left( x \right) + {e^{ – 2x}} = 3{e^{ – x}}\sqrt {f\left( x \right)} .f’\left( x \right),\;\;\forall x \in \left( {2;4} \right)\). Khi đó \(f\left( {\frac{5}{2}} \right)\) thuộc khoảng