Người thợ hồ nâng một xô nước bị rỉ lên cao 20 m với tốc độ cố định

Người thợ hồ nâng một xô nước bị rỉ lên cao 20 m với tốc độ cố định. Cho trọng lượng của xô là ${3 N}$, trọng luợng ban đầu của nước là ${2 N}$. Biết rằng xô nước bị rỉ nên lượng nước trong xô sẽ chảy ra với tốc độ không đổi trong thời gian nâng xô nước lên. Người ta ước tính rằng lượng nước trong xô sẽ thay đổi theo đồ thị là hình bên. Hỏi người thợ hồ đã dùng một công là bao nhiêu đê nâng xô nước lên cao 20m, với giả sử rằng bỏ qua trọng lượng sợi dây?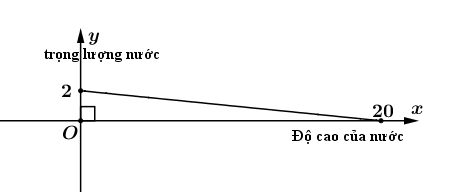
Lời giải
Trả lời: 80 Vì trọng lượng của xô là ${3 N}$ không thay đổi nên công đưa xô lên cao ${20 m}$ là${{W}_{x\hat{o}}}={{P}_{x\hat{o}}}\cdot h=3.20=60(J).$ Trọng lượng của nước thay đổi tùy thuộc vào độ cao của xô so với mặt đất. Gọi ${x}$ là độ cao của xô so với mặt đất, khi đó ${f(x)=a x+b}$ là trọng lượng của nước tương ứng với độ cao ${x}$. Đồ thị hàm số ${f(x)=a x+b}$ đi qua 2 điểm ${A(0 ; 2)}$ và ${B(20 ; 0)}$ nên ${\left\{\begin{array} { l } { a . 0 + b = 2 } \\ { a . 2 0 + b = 0 } \end{array} \Leftrightarrow \left\{\begin{array}{l} b=2 \\ a=-\frac{1}{10} \end{array} \Rightarrow f(x)=-\frac{1}{10} x+2 .\right.\right. }$ Công sinh ra khi đưa nước từ mặt đất lên cao ${20 {~m}}$ là $\int\limits_{0}^{20}{f}(x)dx=\int\limits_{0}^{20}{\left( -\frac{1}{10}x+2 \right)}dx=\left. \left( -\frac{1}{20}{{x}^{2}}+2x \right) \right|_{0}^{20}=20(J).$
Vậy công toàn bộ để đưa cả xô và nước lên cao ${20 {~m}}$ là: $60+20=80(J)\text{. }$