Một khinh khí cầu thay đổi vận tốc lên cao ${v}$ theo biểu đồ bên

Một khinh khí cầu thay đổi vận tốc lên cao ${v}$ theo biểu đồ bên. Nó khởi hành ở độ cao 350 m so với mực nước biển. 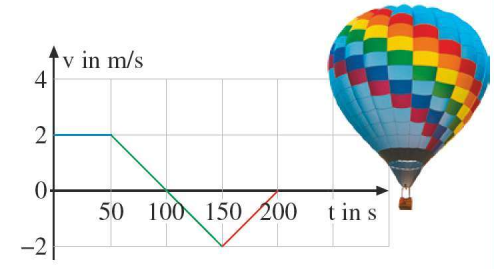Hỏi sau 200 s, khinh khí cầu ở độ cao bao nhiêu mét so với mực nước biển.
Lời giải Từ đồ thị, ta có ba đoạn thẳng và các tập xác định: $v(t)=\left\{ \begin{align} & 2,0\le t\le 50, \\ & -0,04t+4,50\le t\le 150, \\ & 0,04t-8,150\le t\le 200, \\ \end{align} \right.$ ($v$ tính bằng m/s, $t$ tính bằng s) Độ cao tăng thêm là tích phân xác định của ${v}$ trên ${[0 ; 200]}$: $\begin{align} & \int_{0}^{50}{2}dt=\left. 2t \right|_{0}^{50}=100~m \\ & \int_{50}^{150}{(-0,04t+4)}dt=\left. \left[ -0,02{{t}^{2}}+4t \right] \right|_{50}^{150}=0~m \\ & \int_{150}^{200}{(0,04t-8)}dt=\left. \left[ 0,02{{t}^{2}}-8t \right] \right|_{150}^{200}=-50~m \\ \end{align}$
Vậy tổng mức tăng độ cao là ${100+0-50=50 {~m}}$. Sau 200 s, khinh khí cầu ở độ cao ${350+50=400 {~m}}$ so với mực nước biển.