Một lực 30 N cần thiết để kéo giãn một lò xo thêm 4 cm so với chiều dài tự nhiên 18 cm

Một lực 30 N cần thiết để kéo giãn một lò xo thêm 4 cm so với chiều dài tự nhiên 18 cm. Hãy tìm công cần thiết là bao nhiêu Jun (J) để kéo giãn lò xo từ chiều dài 20 cm đến 24 cm.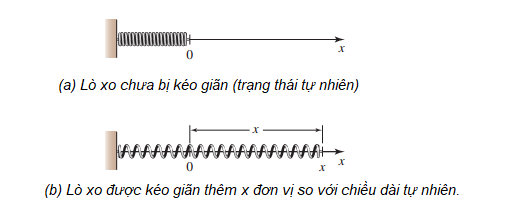
Lời giải
Trả lời: 1,2 Giả sử đặt lò xo trùng với trục ${O x}$ và đầu tự do ở gốc toạ độ (như Hình b). Theo định luật Hooke, lực ${F(x)}$ cần để kéo giãn lò xo thêm ${x}$ mét so với chiều dài tự nhiên là ${F(x)=k x}$. Vì cần lực 30 N để kéo giãn lò xo 4 cm, tức ${0,04 {~m}}$, nên $30=k\cdot 0,04\quad \Rightarrow \quad k=750(~N/m)$ Do đó ${F(x)=750 x}$. Công để kéo giãn từ 20 cm đến 24 cm (tức ${x}$ tăng từ ${0,02 {~m}}$ đến ${0,06 {~m}}$) là $W=\int_{0,02}^{0,06}{F}(x)dx=\int_{0,02}^{0,06}{7}50xdx=750\left. \left[ \frac{1}{2}{{x}^{2}} \right] \right|_{0,02}^{0,06}=375\left( {{(0,06)}^{2}}-{{(0,02)}^{2}} \right)=1,2~J$
Vậy công cần thiết là ${1,2 {~J}}$.