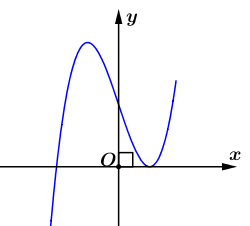
Một đường ray tàu lượn trong khu vui chơi giải trí có hình dáng được mô phỏng theo đồ thị của hàm số $y = x^3 – 3x + 2$, ký hiệu là (C). Để đảm bảo an toàn và tính thẩm mỹ, người ta chọn hai điểm $A(a;b)$ và $B(c;d)$ trên đường ray sao cho tiếp tuyến tại hai điểm này có cùng độ dốc (cùng hệ số góc). Đồng thời, đoạn đường nối hai trụ đỡ tại các điểm A và B phải vuông góc với một đường dây điện có phương trình $x + y – 5 = 0$. Tìm $b+d$

Lời giải
Đáp số: $4$
$y={{x}^{3}}-3x+2\Rightarrow {y}’=3{{x}^{2}}-3$
Tiếp tuyến với $\left( C \right)$ tại $A,B$ có cùng hệ số góc và chỉ khi ${f}’\left( {{x}_{A}} \right)={f}’\left( {{x}_{B}} \right)\Leftrightarrow x_{A}^{2}=x_{B}^{2}\Leftrightarrow \left[ \begin{array}{l}
{{x}_{A}}={{x}_{B}}\left( L \right) \\
{{x}_{A}}+{{x}_{B}}=0 \\
\end{array} \right.$
$\Rightarrow A,B$ đối xứng nhau qua $I\left( 0;2 \right)$ là tâm đối xứng của $\left( C \right).$
$AB\bot d:x+y-5=0\Rightarrow AB:x-y+m=0.$
$AB$ qua $I$ nên ta có $m=2\Rightarrow AB:x-y+2=0.$
Khi đó hoành độ $A,B$ thỏa mãn phương trình
${{x}^{3}}-3x+2=x+2\Leftrightarrow \left[ \begin{array}{l}
x=0\ (L) \\
x=\pm 2 \\
\end{array} \right.\Rightarrow A\left( 2;4 \right),B\left( -2;0 \right)$.
