Một nhà máy sản xuất $x$ sản phẩm trong mỗi tháng. Chi phí sản xuất $x$ sản phẩm được cho bởi hàm chi phí $C\left( x \right)=16000+500x-1,6{{x}^{2}}+0,004{{x}^{3}}$ (nghìn đồng). Biết giá bán của mỗi sản phẩm là một hàm số phụ thuộc vào số lượng sản phẩm $x$ và được cho bởi công thức $p\left( x \right)=1700-7x$ (nghìn đồng). Hỏi mỗi tháng nhà máy nên sản xuất bao nhiêu sản phẩm để lợi nhuận thu được là lớn nhất? Biết rằng kết quả khảo sát thị trường cho thấy sản phẩm sản xuất ra sẽ tiêu thụ hết.
Lời giải
Đáp án: $100$.
+) Số tiền nhà máy thu được khi bán hết $x$ sản phẩm là: $x.p\left( x \right)=1700x-7{{x}^{2}}$ (nghìn đồng)
Lợi nhuận nhà máy thu được khi sản xuất và bán hết $x$ sản phẩm là: $x.p\left( x \right)-C\left( x \right)=-0,004{{x}^{3}}-5,4{{x}^{2}}+1200x-16000$ (với $x{>}0$ ).
+) Xét hàm số $f\left( x \right)=-0,004{{x}^{3}}-5,4{{x}^{2}}+1200x-16000$ trên $\left( 0;+\infty \right)$
Ta có ${f}’\left( x \right)=-0,012{{x}^{2}}-10,8x+1200$; ${f}’\left( x \right)=0\Leftrightarrow \left[ \begin{array}{l}
x=100 \\
x=-1000 \\
\end{array} \right.$
Bảng biến thiên
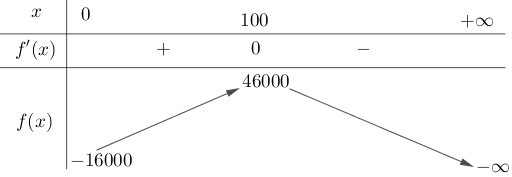
Từ bảng biến thiên, suy ra $\max\limits_{\left( 0;+\infty \right)} f\left( x \right)=f\left( 100 \right)=46000$ (nghìn đồng).
Vậy mỗi tháng nhà máy nên sản xuất $100$ sản phẩm thì lợi nhuận thu được là lớn nhất.

Để lại một bình luận