Một hộ kinh doanh sản xuất mỗi ngày được $x$ sản phẩm, $\left( 1\le x\le 20 \right)$

Một hộ kinh doanh sản xuất mỗi ngày được $x$ sản phẩm, $\left( 1\le x\le 20 \right)$. Chi phí sản xuất $x$ sản phẩm được cho bởi $C\left( x \right)={{x}^{3}}-3{{x}^{2}}+80x+500$ (nghìn đồng). Giả sử hộ kinh doanh này bán mỗi sản phẩm với giá $320$ nghìn đồng. Lợi nhuận lớn nhất mà hộ kinh doanh có được là bao nhiêu triệu đồng? (làm tròn kết quả đến hàng phần mười).

Lời giải

Đáp án: $1,2$.

Doanh thu tối đa mà hộ kinh doanh có thể thu được là $320x$ (nghìn đồng).

Lợi nhuận hộ kinh doanh thu được là $L\left( x \right)=320x-\left( {{x}^{3}}-3{{x}^{2}}+80x+500 \right)=-{{x}^{3}}+3{{x}^{2}}+240x-500$.

Ta có ${L}’\left( x \right)=-3{{x}^{2}}+6x+240=0\Rightarrow \left[ \begin{matrix}

x=10 \\

x=-8. \\

\end{matrix} \right.$

Bảng biến thiên

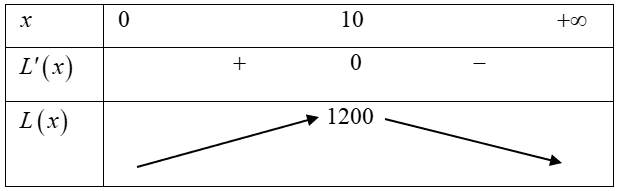
Vậy lợi nhuận lớn nhất mà hộ kinh doanh có được là 1200 nghìn đồng $=1,2$ triệu đồng.