Một doanh nghiệp dự định sản xuất $200$ máy tính bảng dành cho học sinh

Một doanh nghiệp dự định sản xuất $200$ máy tính bảng dành cho học sinh. Nếu doanh nghiệp đó bán $x$ máy tính bảng $\left( 1\le x\le 200,x\in \mathbb{N} \right)$ thì giá bán cho mỗi máy tính bảng là $p\left( x \right)=4000-10x$ (nghìn đồng), trong đó chí phí để sản xuất mỗi máy tính bảng là $c\left( x \right)={{x}^{2}}-70x+400+\dfrac{1000}{x}$ (nghìn đồng). Hỏi doanh nghiệp đó sẽ bán bao nhiêu máy tính bảng để lợi nhuận cao nhất?.

Lời giải

Đáp số: 60.

Ta có doanh thu của doanh nghiệp khi bán $x$ máy tính bảng là: $D\left( x \right)=x.p\left( x \right)=x\left( 4000-10x \right)=4000x-10{{x}^{2}}$.

Chi phí của doanh nghiệp để sản xuất $x$ máy tính bảng là: $C\left( x \right)=x.c\left( x \right)=x\left( {{x}^{2}}-70x+400+\dfrac{1000}{x} \right)={{x}^{3}}-70{{x}^{2}}+400x+1000$.

Lợi nhuận của doanh nghiệp khi bán $x$ máy tính bảng là: $L\left( x \right)=D\left( x \right)-C\left( x \right)=4000x-10{{x}^{2}}-\left( {{x}^{3}}-70{{x}^{2}}+400x+1000 \right)$ $=-{{x}^{3}}+60{{x}^{2}}+3600x-1000$.

Xét hàm $L\left( x \right)=-{{x}^{3}}+60{{x}^{2}}+3600x-1000\left( 1\le x\le 200;x\in \mathbb{N} \right)$.

Có $y’=-3{{x}^{2}}+120x+3600$.

$y’=0\Leftrightarrow \left[ \begin{array}{l}

x=60\left( N \right) \\

x=-20\left( L \right) \\

\end{array} \right.$.

Ta có bảng biến thiên

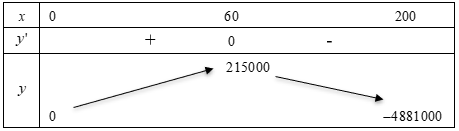
Dựa vào bảng biến thiên ta thấy doanh nghiệp đó sẽ bán $60$ máy tính bảng để lợi nhuận cao nhất.