Nhà máy $A$ chuyên sản xuất một loại sản phẩm cung cấp cho nhà máy $B$

Nhà máy $A$ chuyên sản xuất một loại sản phẩm cung cấp cho nhà máy $B$. Hai nhà máy thỏa thuận rằng, hàng tháng nhà máy $A$ cung cấp cho nhà máy $B$ số lượng sản phẩm theo đơn đặt hàng của $B$ (tối đa $100$ tấn sản phẩm). Nếu số lượng đặt hàng là $x$ tấn sản phẩm thì giá bán cho mỗi tấn sản phẩm là $P\left( x \right)=45-0,001{{x}^{2}}$ (triệu đồng). Chi phí để $A$ sản xuất $x$ tấn sản phẩm trong một tháng là $C\left( x \right)=100+30x$ (triệu đồng) (gồm $100$ triệu đồng chi phí cố định và $30$ triệu đồng cho mỗi tấn sản phẩm). Để mỗi tháng thu được lợi nhuận lớn nhất thì $A$ cần bán cho $B$ bao nhiêu tấn sản phẩm mỗi tháng để lợi nhuận thu được là lớn nhất? (kết quả làm tròn đến hàng đơn vị)

Lời giải

Đáp án: $71$.

Doanh thu khi nhà máy $A$ bán hết $x$ tấn sản phẩm cho nhà máy $B$ là: $x.P\left( x \right)=x\left( 45-0,001{{x}^{2}} \right)=45x-0,001{{x}^{3}}$.

Lợi nhuận thu được là: $L\left( x \right)=45x-0,001{{x}^{3}}-\left( 100+30x \right)$ $=-0,001{{x}^{3}}+15x-100$.

Ta có: ${L}’\left( x \right)=-0,003{{x}^{2}}+15=0\Leftrightarrow \left[ \begin{matrix}

x\approx 70,7 \\

x\approx -70,7 \\

\end{matrix} \right.$

Bảng biến thiên:

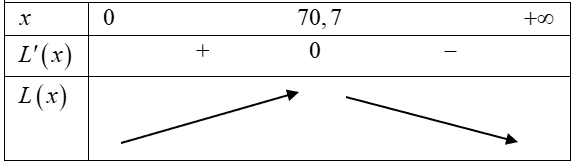
Ta có: $L\left( 70 \right)=607$, $L\left( 71 \right)=607,089{>}L\left( 70 \right)$

Như vậy, nhà máy $A$ cần bán $71$ tấn sản phẩm cho nhà máy $B$ mỗi tháng để lợi nhuận thu được là lớn nhất.