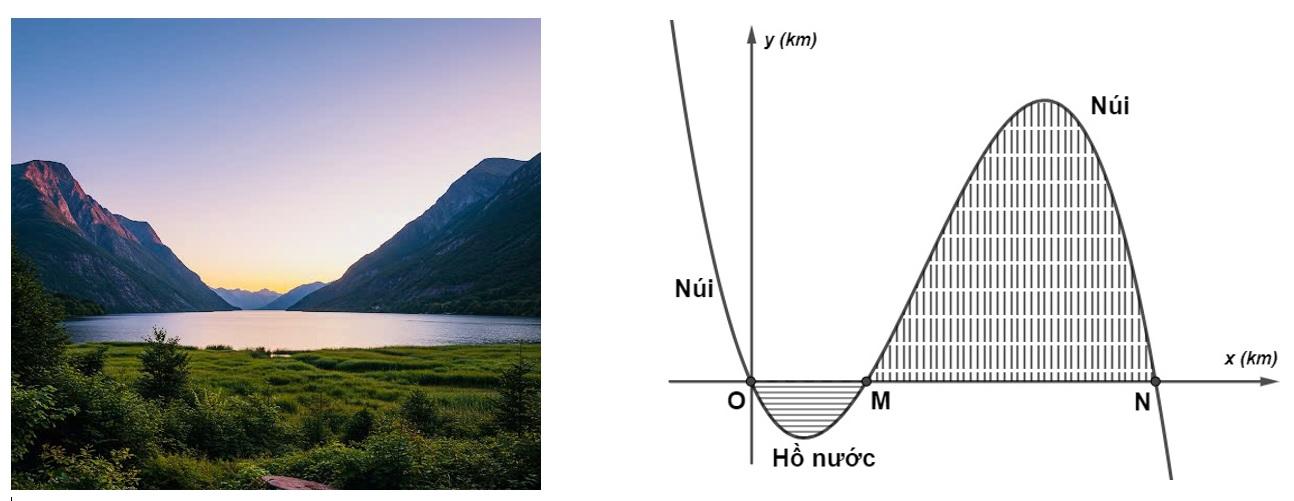
Lát cắt của một vùng đất được mô hình hóa bởi hàm bậc ba $y=f\left( x \right)$ có đồ thị như hình vẽ dưới (đơn vị trên các trục là km). Biết khoảng cách $OM=2km$; độ rộng của núi $MN=3,5km$. Độ sâu của hồ nước là 450m. Chiều cao của ngọn núi là bao nhiêu mét? (làm tròn đến hàng đơn vị).
Lời giải
Đáp số: 1191
Hàm số bậc ba $y=f\left( x \right)$ có dạng $y=a{{x}^{3}}+b{{x}^{2}}+cx+d$, $\left( a\ne 0 \right)$
Ta có: $ON=OM+MN=2+3,5=5,5\left( km \right)$
Dựa vào hình vẽ trên, ta thấy đồ thị hàm số cắt trục hoành tại các điểm: $O\left( 0;0 \right)$, $M\left( 2;0 \right)$ và $N\left( 5,5;0 \right)$
Khi đó, phương trình $f\left( x \right)=0$ có ba nghiệm phân biệt là $x=0;x=2;x=5,5$.
$\Rightarrow f\left( x \right)=k.x\left( x-2 \right)\left( x-5,5 \right)$ $=k\left( {{x}^{3}}-7,5{{x}^{2}}+11x \right)$ với đồ thị hàm số $\lim\limits_{x\to +\infty } =-\infty$ nên $k{<}0$
Ta có: $f’\left( x \right)=k\left( 3{{x}^{2}}-15x+11 \right)$
Xét $f’\left( x \right)=0\Leftrightarrow k\left( 3{{x}^{2}}-15x+11 \right)=0\Leftrightarrow 3{{x}^{2}}-15x+11=0\Leftrightarrow x=\dfrac{15\pm \sqrt{93}}{6}$.
Độ sâu của hồ nước là $450m=0,45km$ nên ta có giá trị cực tiểu của đồ thị hàm số trên là ${{y}_{CT}}=-0,45$.
Suy ra, $f\left( \dfrac{15-\sqrt{93}}{6} \right)=-0,45\Leftrightarrow k.\dfrac{-135+31\sqrt{93}}{36}=-0,45\Leftrightarrow k=\dfrac{-16,2}{-135+31\sqrt{93}}$.
Chiều cao của ngọn núi tương ứng với ${{y}_{C}}=f\left( \dfrac{15+\sqrt{93}}{6} \right)\approx 1,19106\left( km \right)\approx 1191\left( m \right)$.
Vậy ngọn núi cao khoảng $1191m$.
