Một khu vực trồng hoa được xây dựng trong khu du lịch sinh thái

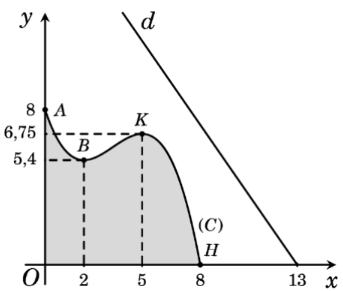
Một khu vực trồng hoa được xây dựng trong khu du lịch sinh thái. Trong mô hình minh họa (như hình vẽ bên), nó được giới hạn bởi các trục tọa độ và đồ thị $\left( C \right)$ của một hàm số bậc ba. Biết rằng đồ thị $\left( C \right)$ đi qua các điểm $A\left( 0;8 \right),B\left( 2;5,4 \right),K\left( 5;6,75 \right)$ và $H\left( 8;0 \right)$. Trong khu du lịch sinh thái có một con đường chạy dọc theo đường thẳng $d:y=-\dfrac{13}{9}x+\dfrac{169}{9}$. Tìm hoành độ của điểm $M$ thuộc $\left( C \right)$ sao cho khoảng cách từ $M$ đến $d$ là nhỏ nhất (làm tròn kết quả đến hàng phần trăm).

Lời giải

Đáp án: 6,16.

Đồ thị $\left( C \right)$ của một hàm số bậc ba có dạng: $f\left( x \right)=a{{x}^{3}}+b{{x}^{2}}+cx+d\ \left( a\ne 0 \right)$.

Vì đồ thị $\left( C \right)$ đi qua các điểm $A\left( 0;8 \right),B\left( 2;5,4 \right),K\left( 5;6,75 \right)$ và $H\left( 8;0 \right)$ nên ta có:

$\left\{ \begin{array}{l}

d=8 \\

8a+4b+2c+d=5,4 \\

125a+25b+5c+d=6,75 \\

512a+64b+8c+d=0 \\

\end{array} \right.\Leftrightarrow \left\{ \begin{array}{l}

a=-\dfrac{1}{10} \\

b=\dfrac{21}{20} \\

c=-3 \\

d=8 \\

\end{array} \right.$.

Suy ra $f\left( x \right)=-\dfrac{1}{10}{{x}^{3}}+\dfrac{21}{20}{{x}^{2}}-3x+8$.

Điểm $M$ thuộc $\left( C \right)$ sao cho khoảng cách từ $M$ đến $d$ là nhỏ nhất khi và chỉ khi tiếp tuyến của $\left( C \right)$ tại $M$ song song với $d$ ( $\left( {{x}_{M}}{>}5 \right)$.

Ta có: ${f}’\left( x \right)=-\dfrac{3}{10}{{x}^{2}}+\dfrac{21}{10}x-3$.

Đường thẳng $d$ có hệ số góc $k=-\dfrac{13}{9}$.

Suy ra: $-\dfrac{3}{10}{{x}^{2}}+\dfrac{21}{10}x-3=-\dfrac{13}{9}\Leftrightarrow \left[ \begin{array}{l}

x=6,16 \\

x=0,84{<}5 \\

\end{array} \right.$.

Do ${{x}_{M}}{>}5$ nên ${{x}_{M}}=6,16$ thỏa mãn.