Một công ty sản xuất một sản phẩm

Một công ty sản xuất một sản phẩm. Bộ phận tài chính của công ty đưa ra hàm giá bán là $p\left( x \right)=1500-30x$, trong đó $p\left( x \right)$ là giá bán của mỗi sản phẩm mà tại giá bán này có $x$ sản phẩm được bán ra.

a) Doanh thu đạt giá trị lớn nhất bằng $18.750.000$.

b) Doanh thu của công ty không phải lúc nào cũng tăng khi số sản phẩm được tiêu thụ.

c) Doanh thu được tính theo công thức: $f(x)=x.p\left( x \right)$.

d) Càng nhiều sản phẩm được tiêu thụ thì giá bán mỗi sản phẩm càng giảm.

Lời giải:
Giá bán 1 sản phẩm khi có $x$ sản phẩm được bán ra là $p\left( x \right)=1500-30x$.
Giá bán $x$ sản phẩm khi có $x$ sản phẩm được bán ra là doanh thu $f\left( x \right)=x.p\left( x \right)=\left( 1500-30x \right).x$.
Xét hàm giá bán $p\left( x \right)=1500-30x$.
Đạo hàm $p’\left( x \right)=-30$.
Hàm giá bán luôn nghịch biến, do đó bán càng nhiều sản phẩm thì giá bán mỗi sản phẩm càng giảm.
Xét hàm doanh thu:
$f\left( x \right)=x.p\left( x \right)=\left( 1500-30x \right).x = 1500x – 30x^2$.
Đạo hàm $f’\left( x \right)=1500-60x$.
Đặt $f’\left( x \right)=0 \Leftrightarrow 1500-60x=0 \Leftrightarrow x=25$.

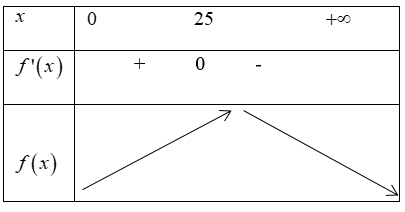
Từ bảng biến thiên, nếu bán từ $25$ sản phẩm trở lên thì doanh thu công ty bắt đầu giảm.
Doanh thu lớn nhất là: $f\left( 25 \right)=1500(25) – 30(25)^2 = 37500 – 30(625) = 37500 – 18750 = 18.750.000$.
(Đúng) Doanh thu đạt giá trị lớn nhất bằng $18.750.000$.
(Vì): Doanh thu lớn nhất đạt được khi $x=25$ sản phẩm, với giá trị là $18.750.000$.
(Đúng) Doanh thu của công ty không phải lúc nào cũng tăng khi số sản phẩm được tiêu thụ.
(Vì): Nếu bán từ $25$ sản phẩm trở lên thì doanh thu công ty bắt đầu giảm.
(Đúng) Doanh thu được tính theo công thức: $f(x)=x.p\left( x \right)$.
(Vì): Doanh thu được tính theo công thức $f\left( x \right)=x.p\left( x \right)$.
(Đúng) Càng nhiều sản phẩm được tiêu thụ thì giá bán mỗi sản phẩm càng giảm.
(Vì): Hàm giá bán luôn nghịch biến, do đó bán càng nhiều sản phẩm thì giá bán mỗi sản phẩm càng giảm.