Gia đình bác Hùng có một ao cá hình chữ nhật

Gia đình bác Hùng có một ao cá hình chữ nhật. Để lắp đặt một hệ thống điện ra vị trí $O$ ở giữa hồ bác dự định nối một đường dây điện từ vị trí $A$ trên bờ hồ đến vị trí $O$ ở giữa hồ . Biết khoảng cách ngắn nhất từ $O$ đến bờ hồ là $OM=84m$, khoảng cách từ $A$ đến $M$ là $AM=112m$. Mỗi mét dây điện lắp đặt ở trên bờ có chi phí cả tiềnn công và tiền vật liệu là $25200$ đồng và mỗi mét dây điện lắp đặt ở dưới nước có chi phí cả tiền công và tiền vật liệu là $42000$ đồng.

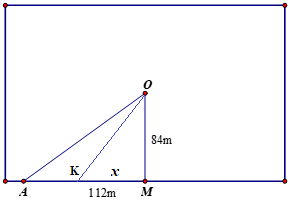
Các mệnh đề sau đúng hay sai?

a) Nếu chọn điểm $K$ cách điểm $A$ một khoảng bằng $49m$ sau đó nối đường dây điện theo đường gấp khúc $AK+KO$ thì chi phí lắp đặt đường dây điện là thấp nhất.
.

b) Nếu chọn một vị trí $K$ trên đoạn $AM$ sao cho $KM=x$ sau đó nối đường dây điện theo đường gấp khúc $AK+KO$ thì chi phí lắp đặt đường dây điện là một hàm số biến $x$ và ta có hàm số là: $f(x)=25200(112-x)+42000\sqrt{{{x}^{2}}+{{84}^{2}}}$.

c) Nếu nối đường dây điện theo đường gấp khúc $AM+MO$ thì chi phí lắp đặt đường dây điện lớn hơn $6000000$ đồng.
.

d) Chi phí thấp nhất để lắp đặt đường dây điện là $5640000$ đồng.
.

Lời giải: Nếu nối đường dây điện theo đường gấp khúc $AM+MO$ thì chi phí lắp đặt đường dây điện là $112.\text{25200+84}\text{.42000}\text{=}\text{6}\text{350}\text{400}$ suy ra mệnh đề 1 sai.
Ta có $AK=112-x$ và $KO=\sqrt{{{x}^{2}}+{{84}^{2}}}$ suy ra chi phí lắp đặt đường dây điện theo đường gấp khúc $AK+KO$ là $f(x)=25200(112-x)+42000\sqrt{{{x}^{2}}+{{84}^{2}}}$ suy ra mệnh đề 2 đúng
Chi phí nối đường dây điện theo đường gấp khúc $AK+KO$ hàm số $f(x)=25200(112-x)+42000\sqrt{{{x}^{2}}+{{84}^{2}}}$, khỏa sát hàm số ta có
$f'(x)=-25200+42000\dfrac{x}{\sqrt{{{x}^{2}}+{{84}^{2}}}}$
$f'(x)=0\Leftrightarrow \dfrac{x}{\sqrt{{{x}^{2}}+{{84}^{2}}}}=\dfrac{25200}{42000}=\dfrac{3}{5}\Leftrightarrow x=\pm 63$
Suy ra $KM=63m,AK=49m$ suy ra mệnh đề 3 sai.
Chi phí lắp đặt thấp nhất là $f(63)=25200(112-63)+42000\sqrt{{{63}^{2}}+{{84}^{2}}}=5644800$
Suy ra mệnh đề 4 đúng.
(Đúng) Nếu chọn điểm $K$ cách điểm $A$ một khoảng bằng $49m$ sau đó nối đường dây điện theo đường gấp khúc $AK+KO$ thì chi phí lắp đặt đường dây điện là thấp nhất.

(Vì): Hàm chi phí là $f(x)=25200(112-x)+42000\sqrt{{{x}^{2}}+{{84}^{2}}}$. Đạo hàm $f'(x)=-25200+42000\dfrac{x}{\sqrt{{{x}^{2}}+{{84}^{2}}}}$. Cho $f'(x)=0 \Leftrightarrow \dfrac{x}{\sqrt{{{x}^{2}}+{{84}^{2}}}}=\dfrac{25200}{42000}=\dfrac{3}{5}$. Giải phương trình ta được $x=63$. Vậy $KM=63m$, khi đó $AK=AM-KM=112-63=49m$. Chi phí thấp nhất khi $AK=49m$.
(Đúng) Nếu chọn một vị trí $K$ trên đoạn $AM$ sao cho $KM=x$ sau đó nối đường dây điện theo đường gấp khúc $AK+KO$ thì chi phí lắp đặt đường dây điện là một hàm số biến $x$ và ta có hàm số là: $f(x)=25200(112-x)+42000\sqrt{{{x}^{2}}+{{84}^{2}}}$.
(Đúng) Nếu nối đường dây điện theo đường gấp khúc $AM+MO$ thì chi phí lắp đặt đường dây điện lớn hơn $6000000$ đồng.

(Vì): Chi phí lắp đặt đường dây điện theo đường gấp khúc $AM+MO$ là $112\cdot25200+84\cdot42000 = 2822400+3528000 = 6350400$ đồng. Vì $6350400 {>} 6000000$ nên mệnh đề này đúng.
(Sai) Chi phí thấp nhất để lắp đặt đường dây điện là $5640000$ đồng.

(Vì): Chi phí thấp nhất là $f(63)=25200(112-63)+42000\sqrt{{{63}^{2}}+{{84}^{2}}}=5644800$ đồng, không phải $5640000$ đồng.