Một khúc gỗ có dạng hình khối nón có bán kính đáy $r=2m$, chiều cao $l=6m$

Một khúc gỗ có dạng hình khối nón có bán kính đáy $r=2m$, chiều cao $l=6m$. Bác thợ mộc chế tác từ khúc gỗ đó thành một khúc gỗ có dạng hình khối trụ như hình vẽ.

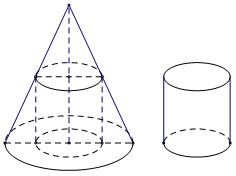
Xét tính đúng sai của các mệnh đề sau:

a) Giả sử bác thợ mộc chế tác khúc gỗ đó thành hình trụ có bán kính đáy bằng chiều cao, khi đó thể tích của khối trụ là $V=\dfrac{27}{8}\pi \left( {{m}^{3}} \right)\cdot.

b) Ta có mặt cắt qua trục hình nón như hình vẽ. Đặt$x$là bán kính đáy hình trụ,$h$là chiều cao của hình trụ.

c) Hàm số xác định thể tích của khối trụ trên là$V=6{{x}^{2}}-3{{x}^{3}}\left( {{m}^{3}} \right),\text{ }\forall x\in \left( 0;2 \right)$.

d) Thể tích lớn nhất của khối gỗ mà bác thợ mộc chế tác là${{V}_{\max }}=\dfrac{32\pi }{9}\left( {{m}^{3}} \right)$.

Lời giải: Ta có mặt cắt qua trục hình nón như hình vẽ. Đặt$x$là bán kính đáy hình trụ,$h$là chiều cao của hình trụ. {}{}{}{}{}{}{}{<}!–{}–{>} Ta có hai tam giác$SAI$và$S{A}'{I}’$đồng dạng. $\Rightarrow \dfrac{SI}{S{I}’}=\dfrac{AI}{{A}'{I}’}\Leftrightarrow \dfrac{6}{6-h}=\dfrac{2}{x}\Rightarrow h=6-3x$, với$0{<}x{<}x{<}x{<}x{<}x{
x=0\left( l \right) \\
x=\dfrac{4}{3}\left( n \right) \\
\end{array} \right.$. Bảng biến thiên: {}{}{}{}{}{}{}{<}!–{}–{>} Dựa vào bảng biến thiên ta thấy${{V}_{\max }}=\dfrac{32\pi }{9}\left( {{m}^{3}} \right)$khi$x=\dfrac{4}{3}$.(Đúng) Giả sử bác thợ mộc chế tác khúc gỗ đó thành hình trụ có bán kính đáy bằng chiều cao, khi đó thể tích của khối trụ là$V=\dfrac{27}{8}\pi \left( {{m}^{3}} \right)\cdot
(Vì): Bác thợ mộc chế tác khúc gỗ đó thành hình trụ có bán kính đáy bằng chiều cao
Suy ra: $x=6-3x\Rightarrow x=\dfrac{3}{2}\Rightarrow V=\pi \cdot \left[ -3{{\left( \dfrac{3}{2} \right)}^{3}}+6{{\left( \dfrac{3}{2} \right)}^{2}} \right]=$, khi đó thể tích của khối trụ là $V=\pi \cdot \left[ -3{{\left( \dfrac{3}{2} \right)}^{3}}+6{{\left( \dfrac{3}{2} \right)}^{2}} \right]=\dfrac{27}{8}\pi \left( {{m}^{3}} \right).$
(Đúng) Ta có mặt cắt qua trục hình nón như hình vẽ. Đặt $x$ là bán kính đáy hình trụ, $h$ là chiều cao của hình trụ.
(Vì): Ta có mặt cắt qua trục hình nón như hình vẽ. Đặt $x$ là bán kính đáy hình trụ, $h$ là chiều cao của hình trụ.
(Đúng) Hàm số xác định thể tích của khối trụ trên là $V=6{{x}^{2}}-3{{x}^{3}}\left( {{m}^{3}} \right),\text{ }\forall x\in \left( 0;2 \right)$.
(Vì): Suy ra: Thể tích của khối trụ là: $V=\pi .{{x}^{2}}.h=\pi .{{x}^{2}}.\left( 6-3x \right)=\pi \left( -3{{x}^{3}}+6{{x}^{2}} \right)$, với $0{<}x{<}2$.
(Đúng) Thể tích lớn nhất của khối gỗ mà bác thợ mộc chế tác là ${{V}_{\max }}=\dfrac{32\pi }{9}\left( {{m}^{3}} \right)$.
(Vì): Dựa vào bảng biến thiên ta thấy ${{V}_{\max }}=\dfrac{32\pi }{9}\left( {{m}^{3}} \right)$ khi $x=\dfrac{4}{3}$.