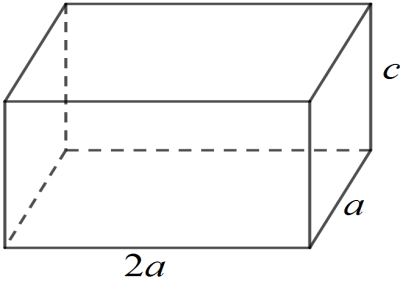
Ông An muốn xây một cái bể chứa nước lớn dạng một khối hộp chữ nhật không nắp có thể tích bằng $288{{\text{m}}^{3}}$. Đáy bể là hình chữ nhật có chiều dài gấp đôi chiều rộng, giá thuê nhân công để xây bể là $500000$ đồng/ ${{\text{m}}^{\text{2}}}$. Ba kích thước của bể được mô tả như hình vẽ dưới $\left( a\left( m \right){>}0,c\left( m \right){>}0 \right)$.
Nếu ông An biết xác định các kích thước của bể hợp lí thì chi phí thuê nhân công sẽ thấp nhất và .
Khi đó:
a) $2{{a}^{2}}c=288$.
b) Diện tích các mặt cần xây là $S=2{{a}^{2}}+4ac+2ac=2{{a}^{2}}+6ac$.
c) Diện tích các mặt cần xây nhỏ nhất là $216{{\text{m}}^{\text{2}}}$.
d) Chi phí thấp nhất để xây dựng bể đó là $100$ triệu đồng.
Lời giải:
Từ hình vẽ ta có ba kích thước của bể là $a$, $2a$, $c$.
Ta có diện tích cách mặt cần xây là $S=2{{a}^{2}}+4ac+2ac=2{{a}^{2}}+6ac$.Thể tích bể $V=a \cdot 2a \cdot c=2{{a}^{2}}c=288\left( 1 \right)$ Từ $\left( 1 \right)$ $\Rightarrow c=\dfrac{144}{{{a}^{2}}}$ nên $S=2{{a}^{2}}+6a \cdot \dfrac{144}{{{a}^{2}}}=2{{a}^{2}}+\dfrac{864}{a}$.
Xét hàm số $S\left( a \right)=2{{a}^{2}}+\dfrac{864}{a}\Rightarrow {S}’\left( a \right)=4a-\dfrac{864}{{{a}^{2}}}$.
${S}’\left( a \right)=0\Leftrightarrow 4a-\dfrac{864}{{{a}^{2}}}=0\Leftrightarrow {{a}^{3}}=216\Leftrightarrow a=6$
Bảng biến thiên của hàm số $S\left( a \right)=2{{a}^{2}}+\dfrac{864}{a}\left( a{>}0 \right)$
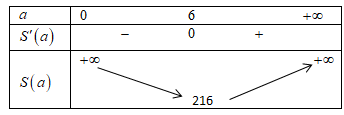
${{S}_{\min }}=216{{m}^{2}}$, khi đó chi phí thấp nhất là $216 \cdot 500000=108$ triệu đồng.
(Đúng) $2{{a}^{2}}c=288$.
(Vì): Thể tích bể là $V=a \cdot 2a \cdot c=2{{a}^{2}}c=288$.
(Đúng) Diện tích các mặt cần xây là $S=2{{a}^{2}}+4ac+2ac=2{{a}^{2}}+6ac$.
(Vì): Diện tích các mặt cần xây là $S=2{{a}^{2}}+4ac+2ac=2{{a}^{2}}+6ac$.
(Đúng) Diện tích các mặt cần xây nhỏ nhất là $216{{\text{m}}^{\text{2}}}$.
(Vì): Từ giải thích, ${{S}_{\min }}=216{{\text{m}}^{\text{2}}}$.
(Sai) Chi phí thấp nhất để xây dựng bể đó là $100$ triệu đồng.
(Vì): Chi phí thấp nhất là $216 \cdot 500000 = 108$ triệu đồng.
