Người ta tiêm một loại thuốc vào mạch máu ở cánh tay phải của một bệnh nhân

Người ta tiêm một loại thuốc vào mạch máu ở cánh tay phải của một bệnh nhân. Sau thời gian là t giờ, nồng độ thuốc hấp thu trong máu của bệnh nhân đó được xác định theo công thức $C(t)=\dfrac{0,28t}{{{t}^{2}}+4}(0{<}t{<}24)$.

a) Nồng độ thuốc hấp thu trong máu của bệnh nhân luôn tăng trong 2 giờ đầu sau khi tiêm.

b) Sau $20$ giờ, nồng độ hấp thu thuốc trong máu của bệnh nhân $C(20)=0,014$.

c) Nồng độ thuốc hấp thu trong máu của bệnh nhân luôn tăng trong $2$ giờ đầu sau khi tiêm.

d) Nồng độ thuốc trong máu bệnh nhân cao nhất là $0,07$.

Lời giải: Xét hàm số $C(t)=\dfrac{0,28t}{{{t}^{2}}+4}$ trên $(0;24)$, có $C'(t)=\dfrac{0,28({{t}^{2}}+4)-0,28t \cdot 2t}{{{({{t}^{2}}+4)}^{2}}}=\dfrac{-0,28{{t}^{2}}+1,12}{{{({{t}^{2}}+4)}^{2}}}$
$C'(t)=0\Leftrightarrow \dfrac{-0,28{{t}^{2}}+1,12}{{{({{t}^{2}}+4)}^{2}}}=0$
$\Leftrightarrow t=2$
Sau $20$ giờ, nồng độ hấp thu thuốc trong máu của bệnh nhân $C(20)=\dfrac{0,28 \cdot 20}{{{20}^{2}}+4}=\dfrac{5,6}{400+4}=\dfrac{5,6}{404}=\dfrac{7}{505}$.
Bảng biến thiên:

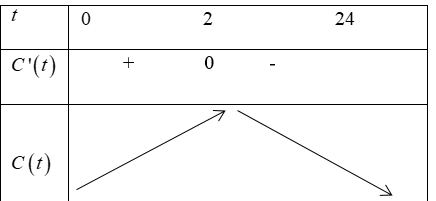
Từ bảng biến thiên, ta thấy hàm số đồng biến trên $(0;2)$ và nghịch biến trên $(2;24)$.
Suy ra $\max\limits_{(0;24)}C(t)=C(2)=\dfrac{0,28 \cdot 2}{2^2+4}=\dfrac{0,56}{8}=0,07.$
(Đúng) Nồng độ thuốc hấp thu trong máu của bệnh nhân luôn tăng trong 2 giờ đầu sau khi tiêm.
(Vì): Nồng độ thuốc tăng trong khoảng $(0;2)$ giờ. Từ bảng biến thiên, ta thấy hàm số đồng biến trên $(0;2)$.
(Sai) Sau $20$ giờ, nồng độ hấp thu thuốc trong máu của bệnh nhân $C(20)=0,014$.
(Vì): Sau $20$ giờ, nồng độ hấp thu thuốc trong máu của bệnh nhân $C(20)=\dfrac{0,28 \cdot 20}{{{20}^{2}}+4}=\dfrac{7}{505} \approx 0,01386 \neq 0,014$.
(Đúng) Nồng độ thuốc hấp thu trong máu của bệnh nhân luôn tăng trong $2$ giờ đầu sau khi tiêm.
(Vì): Hàm số tăng trên $(0;2)$ giờ, do đó luôn tăng trong $2$ giờ đầu.
(Đúng) Nồng độ thuốc trong máu bệnh nhân cao nhất là $0,07$.
(Vì): Từ bảng biến thiên, ta thấy $\max\limits_{(0;24)}C(t)=C(2)=0,07$.