Một công ty bất động sản có 50 căn hộ cho thuê

Một công ty bất động sản có 50 căn hộ cho thuê. Biết rằng nếu cho thuê mỗi căn hộ với giá $2000000$ đồng một tháng thì mọi căn hộ đều có người thuê và cứ mỗi lần tăng giá cho thuê mỗi căn hộ thêm $50000$ đồng một tháng thì có thêm một căn hộ bị bỏ trống. Hỏi :

a) Thu nhập cao nhất công ty có thể đạt được trong 1 tháng là $100000000$ đồng?.

b) Thu nhập cao nhất công ty có thể đạt được trong 1 tháng là $105250000$ đồng?.

c) Có 6 căn hộ bị bỏ trống thì công ty có thu nhập cao nhất ?.

d) Để công ty có thu nhập cao nhất trong 1 tháng thì giá cho thuê là $2250000$ đồng?.

Lời giải: Lời giải
Gọi $x$ $\left( x{>}0 \right)$ là số tiền tăng giá
$\Rightarrow$ Số căn hộ bị bỏ trống là $\dfrac{x}{50000}$ căn hộ
$\Rightarrow$ Số tiền công ty thu được $T\left( x \right)=\left( 2000000+x \right)\left( 50-\dfrac{x}{50000} \right)$
Khảo sát hàm số $T\left( x \right)$ trên $\left( 0;+\infty \right)$
$\Rightarrow$ ${T}’\left( x \right)=10-\dfrac{x}{25000}$ $\Rightarrow$ ${T}’\left( x \right)=0$ $\Leftrightarrow$ $x=250000$.
Bảng biến thiên

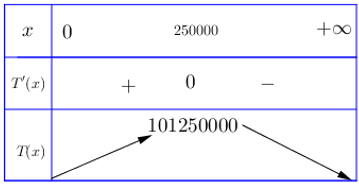
Vậy thu nhập cao nhất công ty có thể đạt được trong 1 tháng là: $T=101250000$.
(Sai) Thu nhập cao nhất công ty có thể đạt được trong 1 tháng là $100000000$ đồng?
(Vì): Thu nhập cao nhất đạt được là $101250000$ đồng.
(Sai) Thu nhập cao nhất công ty có thể đạt được trong 1 tháng là $105250000$ đồng?
(Vì): Thu nhập cao nhất đạt được là $101250000$ đồng.
(Sai) Có 6 căn hộ bị bỏ trống thì công ty có thu nhập cao nhất ?
(Vì): Thu nhập cao nhất khi $x=250000$. Số căn hộ bị bỏ trống là $\dfrac{x}{50000} = \dfrac{250000}{50000} = 5$ căn.
(Đúng) Để công ty có thu nhập cao nhất trong 1 tháng thì giá cho thuê là $2250000$ đồng?
(Vì): Thu nhập cao nhất khi $x=250000$. Khi đó, giá cho thuê là $2000000+x = 2000000+250000=2250000$ đồng.