Cho hàm số $f(x)=-{{x}^{4}}+12{{x}^{2}}+1$, khi đó:

a) Hàm số đồng biến trên khoảng $\left( 1;37 \right)$

Cho hàm số $f(x)=-{{x}^{4}}+12{{x}^{2}}+1$, khi đó:

a) Hàm số đồng biến trên khoảng $\left( 1;37 \right)$.

b) Hàm số có 3 điểm cực trị.

c) Giá trị nhỏ nhất của hàm số $f(x)=-{{x}^{4}}+12{{x}^{2}}+1$ trên đoạn $\left[ -1;2 \right]$ bằng $1$.

d) Giá trị lớn nhất của hàm số $f(x)=-{{x}^{4}}+12{{x}^{2}}+1$ trên đoạn $\left[ -1;2 \right]$ bằng $37$.

Lời giải:
Để phân tích và đánh giá các phát biểu, ta cần tìm đạo hàm và lập bảng biến thiên của hàm số $f(x)=-{{x}^{4}}+12{{x}^{2}}+1$.
Ta có $f'(x) = -4x^3 + 24x$.
Đặt $f'(x)=0 \Leftrightarrow -4x^3 + 24x = 0 \Leftrightarrow -4x(x^2 – 6) = 0 \Leftrightarrow \left[ \begin{array}{l} x=0 \\ x=\sqrt{6} \\ x=-\sqrt{6} \end{array} \right.$.
Bảng biến thiên của hàm số:

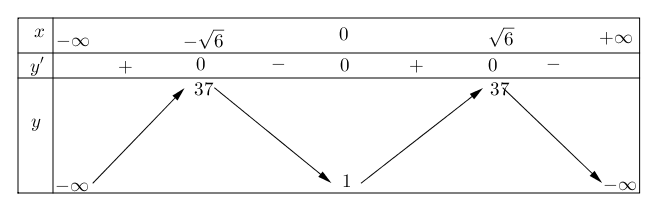
Từ bảng biến thiên, ta thấy:
– Hàm số có 3 điểm cực trị tại $x = -\sqrt{6}, x = 0, x = \sqrt{6}$ do $f'(x)$ đổi dấu qua các điểm này.
– Hàm số đồng biến trên các khoảng $(-\infty; -\sqrt{6})$ và $(0; \sqrt{6})$.

Để tìm giá trị lớn nhất và nhỏ nhất của hàm số trên đoạn $\left[ -1;2 \right]$, ta xét các giá trị của hàm số tại các điểm cực trị thuộc đoạn và tại các mút của đoạn:
Nghiệm của $f'(x)=0$ thuộc đoạn $\left[ -1;2 \right]$ là $x=0$.
Các điểm cần xét: $x=-1$ (mút trái), $x=0$ (điểm cực trị), $x=2$ (mút phải).
$f(-1) = -(-1)^4 + 12(-1)^2 + 1 = -1 + 12 + 1 = 12$.
$f(0) = -(0)^4 + 12(0)^2 + 1 = 1$.
$f(2) = -(2)^4 + 12(2)^2 + 1 = -16 + 12 \cdot 4 + 1 = -16 + 48 + 1 = 33$.
So sánh các giá trị $f(-1)=12$, $f(0)=1$, $f(2)=33$:
– Giá trị lớn nhất của hàm số trên đoạn $\left[ -1;2 \right]$ là $\text{max}\{12, 1, 33\} = 33$.
– Giá trị nhỏ nhất của hàm số trên đoạn $\left[ -1;2 \right]$ là $\text{min}\{12, 1, 33\} = 1$.
(Sai) Hàm số đồng biến trên khoảng $\left( 1;37 \right)$.
(Vì): Ta có $f'(x) = -4x^3 + 24x = -4x(x^2-6)$. Hàm số đồng biến trên các khoảng $(-\infty; -\sqrt{6})$ và $(0; \sqrt{6})$. Khoảng $(1; 37)$ không nằm hoàn toàn trong bất kỳ khoảng đồng biến nào (vì chứa $\sqrt{6} \approx 2.45$ tại đó hàm số đạt cực đại).
(Đúng) Hàm số có 3 điểm cực trị.
(Vì): Ta có $f'(x) = -4x^3 + 24x = -4x(x^2-6)$. Phương trình $f'(x)=0$ có 3 nghiệm phân biệt $x=0, x=\sqrt{6}, x=-\sqrt{6}$. Vì $f'(x)$ đổi dấu khi qua các nghiệm này, nên hàm số có 3 điểm cực trị.
(Đúng) Giá trị nhỏ nhất của hàm số $f(x)=-{{x}^{4}}+12{{x}^{2}}+1$ trên đoạn $\left[ -1;2 \right]$ bằng $1$.
(Vì): Ta có $f'(x) = -4x^3 + 24x$. Trên đoạn $\left[ -1;2 \right]$, $f'(x)=0 \Leftrightarrow x=0$ (nghiệm này thuộc đoạn $[-1;2]$). Các giá trị của hàm số tại các điểm cần xét là $f(-1)=12, f(2)=33, f(0)=1$. So sánh các giá trị này, ta thấy giá trị nhỏ nhất của hàm số trên đoạn $\left[ -1;2 \right]$ là $1$.
(Sai) Giá trị lớn nhất của hàm số $f(x)=-{{x}^{4}}+12{{x}^{2}}+1$ trên đoạn $\left[ -1;2 \right]$ bằng $37$.
(Vì): Ta có $f'(x) = -4x^3 + 24x$. Trên đoạn $\left[ -1;2 \right]$, $f'(x)=0 \Leftrightarrow x=0$ (nghiệm này thuộc đoạn $[-1;2]$). Các giá trị của hàm số tại các điểm cần xét là $f(-1)=12, f(2)=33, f(0)=1$. So sánh các giá trị này, ta thấy giá trị lớn nhất của hàm số trên đoạn $\left[ -1;2 \right]$ là $33$, không phải $37$ (giá trị $37$ đạt được tại $x=\pm\sqrt{6}$ nằm ngoài đoạn $[-1;2]$).