Khi nuôi tôm trong một hồ tự nhiên, một nhà khoa học đã thống kê được rằng: Nếu trên mỗi mét vuông mặt hồ thả $x$ con tôm giống thì cuối vụ mỗi con tôm có cân nặng trung bình là $108-{{x}^{2}}$ (gam)

Khi nuôi tôm trong một hồ tự nhiên, một nhà khoa học đã thống kê được rằng: Nếu trên mỗi mét vuông mặt hồ thả $x$ con tôm giống thì cuối vụ mỗi con tôm có cân nặng trung bình là $108-{{x}^{2}}$ (gam).

a) Điều kiện xác định là $x {

b) Sau một vụ lượng tôm trung bình trên mỗi mét vuông mặt hồ tự nhiên nặng $x+108-{{x}^{2}}$.

c) Để cuối vụ thu hoạch được nhiều tôm nhất trên mỗi mét vuông mặt hồ tự nhiên thì cần thả $6$ con tôm giống.

d) Lượng tôm nhiều nhất cuối vụ có thể thu hoạch được trên mỗi mét vuông mặt hồ tự nhiên là $400$ (gam).

Lời giải: (a) Đúng: Điều kiện xác định là $x\ge 0$
(b) Đúng: Sau một vụ lượng tôm trung bình trên mỗi mét vuông mặt hồ tự nhiên nặng $x\left( 108-{{x}^{2}} \right)$
(c) Sai: Xét hàm số $f\left( x \right)=108x-{{x}^{3}}$ trên khoảng $\left( 0;+\infty \right)$ ta có
${f}’\left( x \right)=108-3{{x}^{2}}=0\Leftrightarrow 108-3{{x}^{2}}=0\Leftrightarrow \left[ \begin{array}{l} x=6 \\ x=-6{

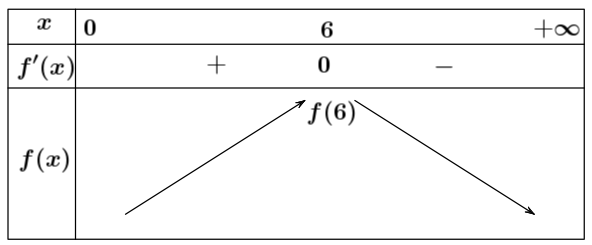
Trên khoảng $\left( 0;+\infty \right)$ hàm số $f\left( x \right)=108x-{{x}^{3}}$ đạt giá trị lớn nhất tại $x=6$.
Vậy nên thả 6 con tôm giống trên mỗi mét vuông mặt hồ thì cuối vụ thu hoạch được nhiều tôm nhất.
(d) Đúng: Lượng tôm nhiều nhất cuối vụ có thể thu hoạch được trên mỗi mét vuông mặt hồ tự nhiên là $f\left( 6 \right)=108.6-{{6}^{3}}=432$ (gam).
(Sai) Điều kiện xác định là $x {
(Vì): $x$ là số con tôm giống nên $x\ge 0$.
(Sai) Sau một vụ lượng tôm trung bình trên mỗi mét vuông mặt hồ tự nhiên nặng $x+108-{{x}^{2}}$.
(Vì): Lượng tôm = (số con tôm) $\times$ (cân nặng trung bình mỗi con) = $x\left( 108-{{x}^{2}} \right)$ (gam).
(Đúng) Để cuối vụ thu hoạch được nhiều tôm nhất trên mỗi mét vuông mặt hồ tự nhiên thì cần thả $6$ con tôm giống.
(Vì): Xét hàm số $f\left( x \right)=108x-{{x}^{3}}$ trên khoảng $\left( 0;+\infty \right)$ ta có ${f}’\left( x \right)=108-3{{x}^{2}}=0\Leftrightarrow x=6$ (vì $x {>} 0$). Hàm số đạt giá trị lớn nhất tại $x=6$.
(Sai) Lượng tôm nhiều nhất cuối vụ có thể thu hoạch được trên mỗi mét vuông mặt hồ tự nhiên là $400$ (gam).
(Vì): Lượng tôm nhiều nhất cuối vụ có thể thu hoạch được trên mỗi mét vuông mặt hồ tự nhiên là $f\left( 6 \right)=108\cdot 6-{{6}^{3}}=432$ (gam).