Cho một tấm nhôm hình vuông có cạnh bằng $30\left( cm \right)$. Người ta cắt ở bốn góc của tấm nhôm đó thành bốn hình vuông bằng nhau, mỗi hình vuông có cạnh $x\left( cm \right)$, rồi gập tấm nhôm lại để thành cái hộp không nắp. Các phát biểu sau đúng hay sai?
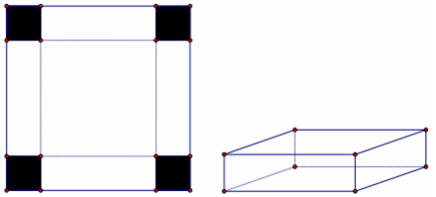
a) Đáy của hộp là một hình vuông có cạnh bằng $30-2x\left( cm \right)$.
b) Nếu $x=3cm$ thì thể tích hộp bằng $1500\left( c{{m}^{3}} \right)$.
c) Thể tích hộp đạt giá trị lớn nhất khi $x=15\left( cm \right)$.
d) Giá trị lớn nhất của hộp bằng $2500c{{m}^{3}}$.
Lời giải: Đáy của hộp là một hình vuông có cạnh bằng $30-2x\left( cm \right)$ Thể tích cái hộp không nắp: $V=x{{\left( 30-2x \right)}^{2}}$
Thể tích hộp nếu $x=3cm$ $V\left( 3 \right)=1728\left( c{{m}^{3}} \right)$ ${V}’=900+12{{x}^{2}}-240x$
${V}’=0\Leftrightarrow \left[ \begin{array}{l} x=15 \\ x=5 \end{array} \right.,x\in \left( 0;15 \right)$
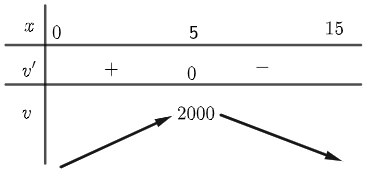
Thể tích hộp đạt giá trị lớn nhất tại $x=5\left( cm \right)$.Thể tích hộp đạt giá trị lớn nhất bằng $V\left( 5 \right)=2000$ $\left( c{{m}^{3}} \right)$.
(Đúng) Đáy của hộp là một hình vuông có cạnh bằng $30-2x\left( cm \right)$
(Vì): Đáy của hộp là một hình vuông có cạnh bằng $30-2x\left( cm \right)$
(Sai) Nếu $x=3cm$ thì thể tích hộp bằng $1500\left( c{{m}^{3}} \right)$.
(Vì): Thể tích cái hộp không nắp: $V=x{{\left( 30-2x \right)}^{2}}$
Thể tích hộp nếu $x=3cm$ $V\left( 3 \right)=1728\left( c{{m}^{3}} \right)$
(Sai) Thể tích hộp đạt giá trị lớn nhất khi $x=15\left( cm \right)$
(Vì): ${V}’=900+12{{x}^{2}}-240x$
${V}’=0\Leftrightarrow \left[ \begin{array}{l} x=15 \\ x=5 \end{array} \right.,x\in \left( 0;15 \right)$
Thể tích hộp đạt giá trị lớn nhất tại $x=5\left( cm \right).$
(Sai) Giá trị lớn nhất của hộp bằng $2500c{{m}^{3}}$.
(Vì): Thể tích hộp đạt giá trị lớn nhất bằng $V\left( 5 \right)=2000$ $\left( c{{m}^{3}} \right).$
