Một người đàn ông muốn chèo thuyền ở vị trí $A$ tới điểm $B$ về phía hạ lưu bờ đối diện, càng nhanh càng tốt, trên một bờ sông thẳng rộng $3\text{km}$ (như hình vẽ)

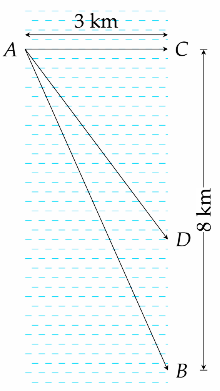
Một người đàn ông muốn chèo thuyền ở vị trí $A$ tới điểm $B$ về phía hạ lưu bờ đối diện, càng nhanh càng tốt, trên một bờ sông thẳng rộng $3\text{km}$ (như hình vẽ). Anh có thể chèo thuyền của mình trực tiếp qua sông để đến $C$ và sau đó chạy đến $B$, hay có thể chèo trực tiếp đến $B$, hoặc anh ta có thể chèo thuyền đến một điểm $D$ giữa $C$ và $B$ và sau đó chạy đến $B$. Biết anh ấy có thể chèo thuyền $6\text{km/}\text{h}$, chạy $8\text{km/}\text{h}$ và quãng đường $BC=8\text{km}$. Biết tốc độ của dòng nước là không đáng kể so với tốc độ chèo thuyền của người đàn ông. Gọi $x\left( \text{km} \right)$ là độ dài quãng đường $BD$. Xét tính đúng sai trong các khẳng định sau:

a) $x\left( \text{km} \right)$ là độ dài quãng đường $CD$.

b) Thời gian chèo thuyền trên quãng đường $AD$ là: $\dfrac{\sqrt{{{x}^{2}}+9}}{3}$ (giờ).

c) Tổng thời gian di chuyển từ $A$ đến $B$ là $\dfrac{\sqrt{{{x}^{2}}+9}}{3}+\dfrac{8-x}{8}$.

d) Khoảng $1$ giờ $20$ phút là khoảng thời gian ngắn nhất để người đàn ông đến $B$.

Lời giải:
Để giải bài toán này, ta sẽ thiết lập một hàm thời gian phụ thuộc vào vị trí $D$.
Gọi $x\left( \text{km} \right)$ là độ dài quãng đường $BD$. Theo hình vẽ và thông tin đề bài, $C$ là điểm đối diện $A$ trên bờ sông, và $BC = 8\text{ km}$. Do $D$ nằm giữa $C$ và $B$, nên độ dài quãng đường $CD = BC – BD = 8 – x\left( \text{km} \right)$.
Khoảng cách từ $A$ đến $C$ (chiều rộng sông) là $3\text{ km}$.
Quãng đường chèo thuyền từ $A$ đến $D$ là cạnh huyền của tam giác vuông tạo bởi $AC$ và $CD$. Sử dụng định lý Pythagoras, ta có:
$AD = \sqrt{AC^2 + CD^2} = \sqrt{3^2 + (8-x)^2} = \sqrt{9+{{(8-x)}^{2}}}\text{ (km)}$.
Tốc độ chèo thuyền của người đàn ông là $6\text{ km/h}$. Thời gian chèo thuyền là $t_{\text{cheo}} = \dfrac{AD}{\text{tốc độ chèo}} = \dfrac{\sqrt{9+{{(8-x)}^{2}}}}{6}$ (giờ).
Tốc độ chạy của người đàn ông là $8\text{ km/h}$. Thời gian chạy trên quãng đường $DB$ là $t_{\text{chay}} = \dfrac{BD}{\text{tốc độ chạy}} = \dfrac{x}{8}$ (giờ).
Tổng thời gian di chuyển từ $A$ đến $B$ là $T\left( x \right) = t_{\text{cheo}} + t_{\text{chay}} = \dfrac{\sqrt{9+{{(8-x)}^{2}}}}{6}+\dfrac{x}{8}$.
Ta cần tìm giá trị nhỏ nhất của hàm số $T\left( x \right)$ trên đoạn $\left[ 0;8 \right]$ (do $D$ nằm giữa $C$ và $B$).
Lấy đạo hàm của $T\left( x \right)$ theo $x$:
${T}’\left( x \right)=\dfrac{1}{6} \cdot \dfrac{2(8-x)(-1)}{2\sqrt{9+{{(8-x)}^{2}}}} + \dfrac{1}{8} = \dfrac{-(8-x)}{6\sqrt{9+{{(8-x)}^{2}}}} + \dfrac{1}{8}$.
Để tìm điểm cực trị, đặt ${T}’\left( x \right)=0$:
$\dfrac{-(8-x)}{6\sqrt{9+{{(8-x)}^{2}}}} + \dfrac{1}{8} = 0 \Leftrightarrow \dfrac{8-x}{6\sqrt{9+{{(8-x)}^{2}}}} = \dfrac{1}{8}$.
$\Leftrightarrow 8(8-x) = 6\sqrt{9+{{(8-x)}^{2}}} \Leftrightarrow 4(8-x) = 3\sqrt{9+{{(8-x)}^{2}}}$.
Bình phương hai vế (với điều kiện $8-x \ge 0$, và $\sqrt{9+(8-x)^2}$ luôn dương):
$16{{(8-x)}^{2}} = 9(9+{{(8-x)}^{2}})$.
$16{{(8-x)}^{2}} = 81 + 9{{(8-x)}^{2}}$.
$7{{(8-x)}^{2}} = 81 \Rightarrow (8-x)^2 = \dfrac{81}{7}$.
Vì $8-x \ge 0$ (do $x \le 8$), ta lấy căn bậc hai:
$8-x = \dfrac{9}{\sqrt{7}} \Rightarrow x = 8 – \dfrac{9}{\sqrt{7}}$.
Để xác định giá trị nhỏ nhất, ta xét các giá trị của $T(x)$ tại các điểm mút và điểm cực trị.
Tại $x=0$ (người đàn ông chèo đến $C$ rồi chạy đến $B$):
$T(0) = \dfrac{\sqrt{9+(8-0)^2}}{6}+\dfrac{0}{8} = \dfrac{\sqrt{9+64}}{6} = \dfrac{\sqrt{73}}{6} \approx 1,424\text{ giờ}$.
Tại $x=8$ (người đàn ông chèo thẳng đến $B$):
$T(8) = \dfrac{\sqrt{9+(8-8)^2}}{6}+\dfrac{8}{8} = \dfrac{\sqrt{9}}{6}+1 = \dfrac{3}{6}+1 = \dfrac{1}{2}+1 = \dfrac{3}{2} = 1,5\text{ giờ}$.
Tại $x = 8 – \dfrac{9}{\sqrt{7}}$ (điểm cực trị):
$T\left( 8-\dfrac{9}{\sqrt{7}} \right) = \dfrac{\sqrt{9+\left(\dfrac{9}{\sqrt{7}}\right)^2}}{6}+\dfrac{8-\dfrac{9}{\sqrt{7}}}{8}$.
Thế $8-x = \dfrac{9}{\sqrt{7}}$ vào biểu thức:
$T\left( 8-\dfrac{9}{\sqrt{7}} \right) = \dfrac{\sqrt{9+\dfrac{81}{7}}}{6} + \left(1-\dfrac{9}{8\sqrt{7}}\right)$
$= \dfrac{\sqrt{\dfrac{63+81}{7}}}{6} + 1-\dfrac{9}{8\sqrt{7}} = \dfrac{\sqrt{\dfrac{144}{7}}}{6} + 1-\dfrac{9}{8\sqrt{7}}$
$= \dfrac{\frac{12}{\sqrt{7}}}{6} + 1-\dfrac{9}{8\sqrt{7}} = \dfrac{2}{\sqrt{7}} + 1-\dfrac{9}{8\sqrt{7}}$
$= \dfrac{16}{8\sqrt{7}} + 1-\dfrac{9}{8\sqrt{7}} = 1 + \dfrac{7}{8\sqrt{7}} = 1 + \dfrac{\sqrt{7}}{8}\text{ giờ}$.
Giá trị này xấp xỉ $1+\dfrac{2,64575}{8} \approx 1+0,3307 = 1,3307\text{ giờ}$.
So sánh ba giá trị: $1,424\text{ giờ}$, $1,5\text{ giờ}$, $1,3307\text{ giờ}$.
Thời gian ngắn nhất là $1+\dfrac{\sqrt{7}}{8}\text{ giờ}$.
Đổi sang định dạng giờ và phút: $1+\dfrac{\sqrt{7}}{8}\text{ giờ} \approx 1\text{ giờ } (0,3307 \times 60)\text{ phút} \approx 1\text{ giờ } 19,84\text{ phút} \approx {{1}^{\text{h}}}2{0}’$.
(Sai) $x\left( \text{km} \right)$ là độ dài quãng đường $CD$.
(Vì): Gọi $x\left( \text{km} \right)$ là độ dài quãng đường $BD$; do $BC=8\text{ km}$ nên $CD=BC-BD=8-x\left( \text{km} \right)$ là độ dài quãng đường $CD$.
(Sai) Thời gian chèo thuyền trên quãng đường $AD$ là: $\dfrac{\sqrt{{{x}^{2}}+9}}{3}$ (giờ).
(Vì): Quãng đường chèo thuyền $AD = \sqrt{AC^2+CD^2} = \sqrt{3^2+(8-x)^2} = \sqrt{9+{{(8-x)}^{2}}}$. Tốc độ chèo thuyền là $6\text{ km/h}$. Vậy thời gian chèo thuyền là $\dfrac{\sqrt{9+{{(8-x)}^{2}}}}{6}$ (giờ).
(Sai) Tổng thời gian di chuyển từ $A$ đến $B$ là $\dfrac{\sqrt{{{x}^{2}}+9}}{3}+\dfrac{8-x}{8}$.
(Vì): Tổng thời gian di chuyển từ $A$ đến $B$ là $T\left( x \right)=\dfrac{\sqrt{9+{{(8-x)}^{2}}}}{6}+\dfrac{x}{8}$.
(Đúng) Khoảng $1$ giờ $20$ phút là khoảng thời gian ngắn nhất để người đàn ông đến $B$.
(Vì): Dựa vào kết quả tính toán, thời gian ngắn nhất để di chuyển từ $A$ đến $B$ là $1+\dfrac{\sqrt{7}}{8}$. Vậy khoảng thời gian ngắn nhất để người đàn ông đến $B$ là $1+\dfrac{\sqrt{7}}{8}\approx {{1}^{\text{h}}}2{0}’$.