Từ một tấm bìa hình vuông $ABCD$ có cạnh bằng $M{{A}^{2}}=M{{B}^{2}}+M{{C}^{2}}$ người ta cắt bỏ bốn tam giác cân bằng nhau là $AMB$, $BNC$, $CPD$ và $DQA$

Từ một tấm bìa hình vuông $ABCD$ có cạnh bằng $M{{A}^{2}}=M{{B}^{2}}+M{{C}^{2}}$ người ta cắt bỏ bốn tam giác cân bằng nhau là $AMB$, $BNC$, $CPD$ và $DQA$. Với phần còn lại người ta gấp lên và ghép lại để thành hình chóp tứ giác đều.

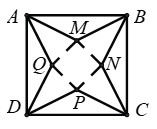
Gọi cạnh đáy của mô hình là $x$ (cm) với $x{>}0$.

a) Chiều cao của hình chóp là $\sqrt{1200-25\sqrt{2}x}$.

b) Điều kiện của $x$ là: $0{<}x{<}25\sqrt{2}$.

c) Thể tích của khối chóp bằng $\dfrac{1}{3}.\sqrt{1250{{x}^{4}}-25\sqrt{2}{{x}^{5}}}$.

d) Khi cạnh đáy của khối chóp bằng $3\sqrt{2}\text{dm}$ thì thể tích của khối chóp là lớn nhất.

Lời giải:

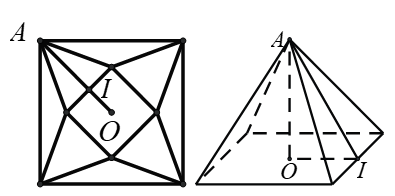
(a) Đúng : Gọi cạnh đáy của mô hình là $x$ (cm) với $x{>}0$. Ta có $AI=AO-IO$ $=25\sqrt{2}-\dfrac{x}{2}$.
Chiều cao của hình chóp $h=\sqrt{A{{I}^{2}}-O{{I}^{2}}}=\sqrt{{{\left( 25\sqrt{2}-\dfrac{x}{2} \right)}^{2}}-{{\left( \dfrac{x}{2} \right)}^{2}}}=\sqrt{1250-25\sqrt{2}x}$.
(b) Đúng: Điều kiện $1250-25\sqrt{2}x{>}0$ $\Rightarrow x{
(c) Sai: Thể tích của khối chóp bằng $V=\dfrac{1}{3}.{{x}^{2}}.\sqrt{1250-25\sqrt{2}x}$ $=\dfrac{1}{3}.\sqrt{1250{{x}^{4}}-25\sqrt{2}{{x}^{5}}}$.
(d) Sai: Xét hàm số $y=\dfrac{1}{3}.\sqrt{1250{{x}^{4}}-25\sqrt{2}{{x}^{5}}}$ với $0{<}x{
Ta có ${y}’=\dfrac{1}{3}.\dfrac{5000{{x}^{3}}-125\sqrt{2}{{x}^{4}}}{2\sqrt{1250{{x}^{4}}-25\sqrt{2}{{x}^{3}}}}$; ${y}’=0$ $\Rightarrow 5000{{x}^{3}}-125\sqrt{2}{{x}^{4}}=0$ $\Rightarrow x=20\sqrt{2}$.
Bảng biến thiên

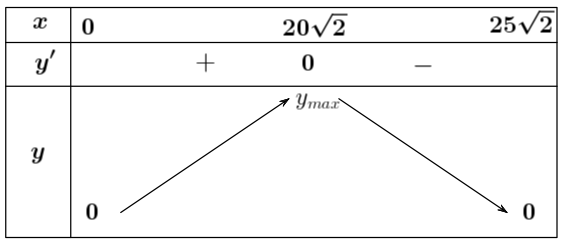
Vậy để mô hình có thể tích lớn nhất thì cạnh đáy của mô hình bằng $20\sqrt{2}\text{cm}$ $=2\sqrt{2}\text{dm}$.
(Sai) Chiều cao của hình chóp là $\sqrt{1200-25\sqrt{2}x}$.
(Đúng) Điều kiện của $x$ là: $0{<}x{<}25\sqrt{2}$
(Đúng) Thể tích của khối chóp bằng $\dfrac{1}{3}.\sqrt{1250{{x}^{4}}-25\sqrt{2}{{x}^{5}}}$.
(Sai) Khi cạnh đáy của khối chóp bằng $3\sqrt{2}\text{dm}$ thì thể tích của khối chóp là lớn nhất